题目内容
【题目】在长方形ABCD内，将两张边长分别为a和b（a＞b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S1，图2中阴影部分的面积为S2．当AD﹣AB=2时，S2﹣S1的值为_______．（用a、b的代数式表示）
【答案】2b
【解析】
利用面积的和差分别表示出S1和S2，然后利用整式的混合运算计算它们的差．
S1=（AB-a）a+（CD-b）（AD-a）=（AB-a）a+（AB-b）（AD-a），
S2=AB（AD-a）+（a-b）（AB-a），
∴S2-S1=AB（AD-a）+（a-b）（AB-a）-（AB-a）a-（AB-b）（AD-a）=（AD-a）（AB-AB+b）+（AB-a）（a-b-a）=bAD-ab-bAB+ab=b（AD-AB）=2b．
故答案为：2b.
练习册系列答案
智慧小复习系列答案
相关题目
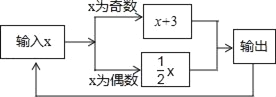
【题目】有一数值转换器，原理如图所示，
（1）如果开始输入x的值是1，可发现第一次输出的是4，第二次输出的是 ，第三次输出的是 ，第4次输出的是 …，请根据你的发现填写如表：
输出次数 | 1 | 2 | 3 | 4 | 5 | … | 3n | 3n+1 | 3n+2 |
输出的数 | 4 |
| 1 |
|
| … |
|
|
|
（2）如果开始输入的数是11，可发现第一次输出的是14，第二次输出的是7，…“，请你探索第2017次和2018次输出的结果．
