Question

（本题8分）如图，在梯形ABCD中，AD//BC，E是AD的中点，BC=5，AD=12，梯形高为4，∠A =45°，P为AD边上的动点.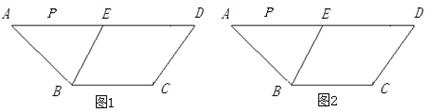

（1）当PA的值为____________时，以点P、B、C、E为顶点的四边形为直角梯形；
（2）当PA的值为____________时，以点P、B、C、E为顶点的四边形为平行四边形；
（3）点P在AD边上运动的过程中，以P、B、C、E为顶点的四边形能否构成菱形？如果能，求出PA长．如果不能，也请说明理由.

Answer 1

（1）4或者9（2）1或11（3）见解析

解析试题分析：
解：25.（1）4或者9  …………2分  
（2）1或11   …………4分    （对1个得1分全对2分）
（3）①由（2）可知当PA=1时，四边形PBCE是平行四边形过点B作BF垂直AD，垂足为F，过点C作BG垂直AD，垂足为G
∵∠A =45°梯形高为4∴可得AF=4，则EF=2，又∵FG=5∴EG=3，由勾股定理可CE=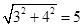  ∴ CE=BC∴四边形PBCE是菱形 …………6分
②由（2）可知当PA=11时，四边形PEBC是平行四边形
由上题可知EF=2，BF=4，由勾股定理可得BE=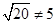  不合题意舍去………8分
考点：平行四边形的判定，菱形的性质
点评：本题属于灵活变换类试题，其中，菱形的基本性质和判定要熟练把握，勾股定理和其逆定理也是考察的重点