题目内容
如图,在直角梯形 中,
中,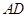 ∥
∥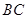 ,
,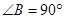 ,
,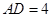 ,
,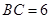 ,
, =
=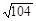 ,点
,点 在
在 上,
上,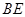 =4.
=4.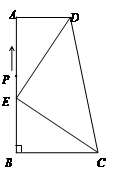
(1)线段 = ;
= ;
(2)试判断△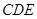 的形状,并说明理由;
的形状,并说明理由;
(3)现有一动点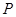 在线段
在线段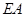 上从点
上从点 开始以每秒1个单位长度的速度向终点
开始以每秒1个单位长度的速度向终点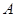 移动,设移动时间为
移动,设移动时间为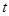 秒(
秒(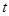 >0).问是否存在
>0).问是否存在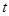 的值使得△
的值使得△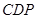 为直角三角形?若存在直接写出
为直角三角形?若存在直接写出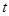 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)10 (2)等腰直角三角形,证明三角形为等腰直角三角形,即只需证明两边相等,且这两边的夹角为90度。
(3)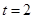 或
或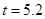
解析试题分析:(1)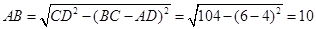
(2)∵在△BEC中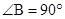
∴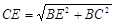 =
=
∵在△AED中,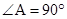 ,
,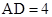
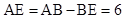
∴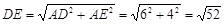
∴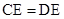
∵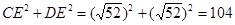
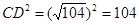
∴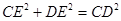
∴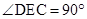
∴△CDE的形状是等腰直角三角形
(3)直角三角形可能有以下两种情况,即 或
或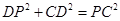
若 ,此时
,此时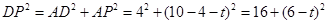 ,
,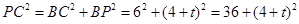 ,
,
所以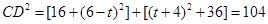 ,解得
,解得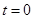 或
或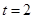 ,又
,又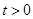 ,所以
,所以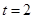
若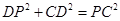 ,根据上面类似方法,可得
,根据上面类似方法,可得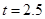
考点:勾股定理的应用
点评:作为试卷的压轴题,最后一问比较难,但是通过观察,可以发现利用勾股定理,求出相应的关系

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 20、如图,在直角梯形中,底AD=6 cm,BC=11 cm,腰CD=12 cm,则这个直角梯形的周长为
20、如图,在直角梯形中,底AD=6 cm,BC=11 cm,腰CD=12 cm,则这个直角梯形的周长为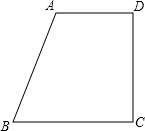 如图,在直角梯形中,AD=6cm,BC=11cm,CD=12cm,则AB的长为
如图,在直角梯形中,AD=6cm,BC=11cm,CD=12cm,则AB的长为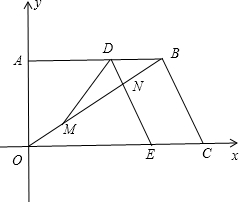 DE由CB出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM.若没运动时间为t(s)(0<t<8).
DE由CB出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM.若没运动时间为t(s)(0<t<8). 如图,在直角梯形中,上底AC=6cm,下底BD=11cm,CD⊥BD且腰CD=12cm,则这个直角梯形的周长为
如图,在直角梯形中,上底AC=6cm,下底BD=11cm,CD⊥BD且腰CD=12cm,则这个直角梯形的周长为 中,
中,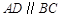 ,
, ,
, ,
, .
. 边上一点,过点
边上一点,过点 作EF⊥DC于点F.求证
作EF⊥DC于点F.求证 .
.