题目内容
如图,在直角梯形中OABC,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O出发沿OB方向匀速运动,速度为1单位/秒;同时,线段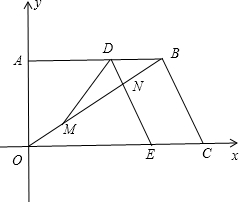 DE由CB出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM.若没运动时间为t(s)(0<t<8).
DE由CB出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM.若没运动时间为t(s)(0<t<8).(1)当t为何值时,以B、D、M为顶点的三角形△OAB与相似?
(2)设△DMN的面积为y,求y与t之间的函数关系式;
(3)连接ME,在上述运动过程中,五边形MECBD的面积是否总为定值?若是,求出此定值;若不是,请说明理由.
分析:(1)首先用t表示出BD、BM的长,由于△BDM、△AOB共用∠ABO,若以B、D、M为顶点的三角形△OAB与相似,则有两种情况:①△BAO∽△BDM,②△BAO∽△BMD;可根据不同相似三角形所得的不同比例线段求出t的值.
(2)过M作MF⊥AB于F,易证得△BFM∽△BAO,即可根据相似三角形所得比例线段求得MF的长,进而可得到△BDM的面积表达式;由于∠BDN=∠OED=∠OCB,易证得△BDN∽△OBC,可求得△BOC的面积,根据相似三角形的面积比等于相似比的平方,即可得到△BDN的面积,然后分两种情况讨论:
①M点在线段ON上,此时0<t≤5,△DMN的面积为△BDM的面积减去△BDN的面积,由此得到y、t的关系式;
②M点在线段BN上,此时5<t<8,△DMN的面积为△BDN的面积减去△BDM的面积,由此得到y、t的关系式.
(3)易求得OB=OC=10,即可知BM=OE=10-t,而BD=OM=t,且∠DBM=∠MOE,即可证得△BDM≌△OME,因此五边形的面积可转化为△OBC的面积,因此五边形的面积是定值,以OC为底、OA为高,即可求得△OCB的面积,也就是这个定值的大小.
(2)过M作MF⊥AB于F,易证得△BFM∽△BAO,即可根据相似三角形所得比例线段求得MF的长,进而可得到△BDM的面积表达式;由于∠BDN=∠OED=∠OCB,易证得△BDN∽△OBC,可求得△BOC的面积,根据相似三角形的面积比等于相似比的平方,即可得到△BDN的面积,然后分两种情况讨论:
①M点在线段ON上,此时0<t≤5,△DMN的面积为△BDM的面积减去△BDN的面积,由此得到y、t的关系式;
②M点在线段BN上,此时5<t<8,△DMN的面积为△BDN的面积减去△BDM的面积,由此得到y、t的关系式.
(3)易求得OB=OC=10,即可知BM=OE=10-t,而BD=OM=t,且∠DBM=∠MOE,即可证得△BDM≌△OME,因此五边形的面积可转化为△OBC的面积,因此五边形的面积是定值,以OC为底、OA为高,即可求得△OCB的面积,也就是这个定值的大小.
解答:解:(1)若△BAO∽△BDM,则
=
,(1分)
即
=
,解得t=
;(2分)
若△BAO∽△BMD,
=
,(3分)
即
=
,解得t=
;(4分)
所以当t=
或t=
时,以B,D,M为顶点的三角形与△OAB相似.
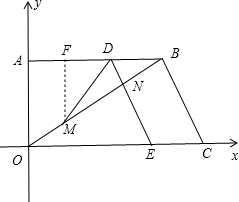 (2)过点M作MF⊥AB于F,则△BFM∽△BAO;
(2)过点M作MF⊥AB于F,则△BFM∽△BAO;
从而
=
,所以MF=6-
t,(5分)
S△BDM=
BD•MF=
t(6-
t),(6分)
△BDN∽△OBC,S△OBC=
×10×6=30,
=(
)2,所以S△BDN=
t2(7分)
①当0<t≤5时,y=S△DMN=S△BDM-S△BDN=
t(6-
t)-
t2=-
t2+3t;
②当5<t<8时,y=S△DMN=S△BDN-S△BDM=
t2-
t(6-
t)=
t2-3t.(8分)
(3)在△BDM与△OME中,
BD=OM=t,∠MBD=∠EOM,BM=EO=10-t,
所以△BDM≌△OME;(9分)
从而五边形MECBD的面积等于三角形OBC的面积,因此它是一个定值,
SMECBD=30.(10分)
| BA |
| BD |
| BO |
| BM |
即
| 8 |
| t |
| 10 |
| 10-t |
| 40 |
| 9 |
若△BAO∽△BMD,
| BA |
| BM |
| BO |
| BD |
即
| 8 |
| 10-t |
| 10 |
| t |
| 50 |
| 9 |
所以当t=
| 40 |
| 9 |
| 50 |
| 9 |
 (2)过点M作MF⊥AB于F,则△BFM∽△BAO;
(2)过点M作MF⊥AB于F,则△BFM∽△BAO;从而
| MF |
| 6 |
| 10-t |
| 10 |
| 3 |
| 5 |
S△BDM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
△BDN∽△OBC,S△OBC=
| 1 |
| 2 |
| S△BDN |
| S△OBC |
| t |
| 10 |
| 3 |
| 10 |
①当0<t≤5时,y=S△DMN=S△BDM-S△BDN=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 3 |
| 5 |
②当5<t<8时,y=S△DMN=S△BDN-S△BDM=
| 3 |
| 10 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
(3)在△BDM与△OME中,
BD=OM=t,∠MBD=∠EOM,BM=EO=10-t,
所以△BDM≌△OME;(9分)
从而五边形MECBD的面积等于三角形OBC的面积,因此它是一个定值,
SMECBD=30.(10分)
点评:此题考查的知识点有:直角梯形的性质、相似三角形及全等三角形的判定和性质、图形面积的求法等知识,(2)题中一定要根据M、N的不同位置分类讨论,以免漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 20、如图,在直角梯形中,底AD=6 cm,BC=11 cm,腰CD=12 cm,则这个直角梯形的周长为
20、如图,在直角梯形中,底AD=6 cm,BC=11 cm,腰CD=12 cm,则这个直角梯形的周长为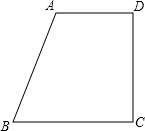 如图,在直角梯形中,AD=6cm,BC=11cm,CD=12cm,则AB的长为
如图,在直角梯形中,AD=6cm,BC=11cm,CD=12cm,则AB的长为 如图,在直角梯形中,上底AC=6cm,下底BD=11cm,CD⊥BD且腰CD=12cm,则这个直角梯形的周长为
如图,在直角梯形中,上底AC=6cm,下底BD=11cm,CD⊥BD且腰CD=12cm,则这个直角梯形的周长为 中,
中, ,
, ,
, ,
, .
. 边上一点,过点
边上一点,过点 作EF⊥DC于点F.求证
作EF⊥DC于点F.求证 .
.