题目内容
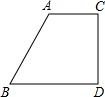如图，在直角梯形中，上底AC=6cm，下底BD=11cm，CD⊥BD且腰CD=12cm，则这个直角梯形的周长为42
42
cm．分析：过A作AE⊥BD于E，得出矩形AEDC，推出AC=DE=6cm，DC=AE=12cm，求出BE，根据勾股定理求出AB，即可求出答案．
解答：解：
过A作AE⊥BD于E，
∵CD⊥BD，
∴∠AEB=∠AED=∠D=90°，AE∥DC，
∵AC∥BD，
∴四边形AEDC是矩形，
∴AC=DE=6cm，DC=AE=12cm，
∵BD=11cm，
∴BE=11cm-6cm=5cm，
在Rt△AEB中，由勾股定理得：AB=
=13（cm），
∴直角梯形ABDC的周长是：AB+BD+CD+AC=13cm+11cm+12cm+6cm=42cm，
故答案为：42．
过A作AE⊥BD于E，
∵CD⊥BD，
∴∠AEB=∠AED=∠D=90°，AE∥DC，
∵AC∥BD，
∴四边形AEDC是矩形，
∴AC=DE=6cm，DC=AE=12cm，
∵BD=11cm，
∴BE=11cm-6cm=5cm，
在Rt△AEB中，由勾股定理得：AB=
| 122+52 |
∴直角梯形ABDC的周长是：AB+BD+CD+AC=13cm+11cm+12cm+6cm=42cm，
故答案为：42．
点评：本题考查了直角梯形的性质，勾股定理，矩形的性质和判定，关键是把直角梯形转化成矩形和直角三角形．
练习册系列答案
相关题目
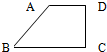20、如图，在直角梯形中，底AD=6 cm，BC=11 cm，腰CD=12 cm，则这个直角梯形的周长为
如图，在直角梯形中，AD=6cm，BC=11cm，CD=12cm，则AB的长为
DE由CB出发沿BA方向匀速运动，速度为1单位/秒，交OB于点N，连接DM．若没运动时间为t（s）（0＜t＜8）．
中，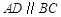
，
，
，
．
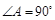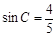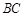边上一点，过点
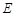作EF⊥DC于点F.求证
．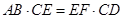