��Ŀ����
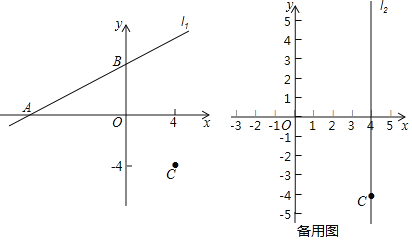
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��l1��y��![]() x+b��x�ύ�ڵ�A����y�ύ�ڵ�B���ҵ�C������Ϊ��4����4����
x+b��x�ύ�ڵ�A����y�ύ�ڵ�B���ҵ�C������Ϊ��4����4����
��1����A������Ϊ�� ������B������Ϊ�� �������ú�b��ʽ�ӱ�ʾ��
��2����b��4ʱ����ͼ��ʾ������AC��BC���ж���ABC����״����֤����Ľ��ۣ�
��3������C��ƽ����y���ֱ��l2����P��ֱ��l2�ϣ�����5��b��4ʱ����ֱ��l1ƽ�ƵĹ����У������ڵ�Pʹ����ABP����ABΪֱ�DZߵĵ���ֱ�������Σ���ֱ��д���������������ĵ�P�������꣮
���𰸡���1������2b��0������0��b������2����ABC�ǵ���ֱ�������Σ����ɼ���������3�����ڣ����������ĵ�P����Ϊ��4����![]() ����4��8����4����12�������ɼ�����
����4��8����4����12�������ɼ�����
��������
��1���ɴ���ϵ�������ɽ�����⣻
��2����ABC�ǵ���ֱ�������Σ������������빫ʽ�Լ����ɶ������涨�������жϣ�
��3��������������ͼ2�У���AB��AP����BAP��90������ֱ��l2��x����N����OB��m����OA��2m������ȫ�������ε����ʣ��������̽�����⣮����ͼ3�У���AB��AP������BAP����90��ʱ����OB��m��OA��2m������ȫ�������ε����ʹ������̽�����⣮����ͼ3�У���AB��PB����ABP��90��ʱ��ͬ���ɵ�.
�⣺��1������ֱ��y��![]() x+b����x��0���õ�y��b����y��0���õ�x����2b��
x+b����x��0���õ�y��b����y��0���õ�x����2b��
��A����2b��0����B��0��b��
�ʴ�Ϊ����2b��0������0��b����
��2����ABC�ǵ���ֱ�������Σ�
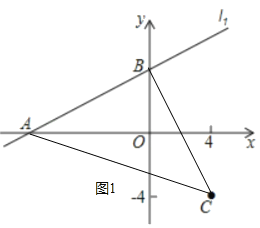
���ɣ���b��4��
��A����8��0����B��0��4������C��4����4����
��AB��![]() ��
��
��AB��BC��
��AB2+BC2����4![]() ��2+��4
��2+��4![]() ��2��160��AC2��160��
��2��160��AC2��160��
��AB2+BC2��AC2��
���ABC��90����
���ABC�ǵ���ֱ�������Σ�
��3������ͼ2�У���AB��AP����BAP��90������ֱ��l2��x����N��
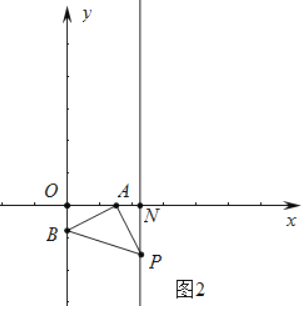
��OA��2OB����OB��m����OA��2m��
����AOB�ա�PNA���ɵ�AN��OB��m��PN��OA��2m��
��ON��3m��4��
��m��![]() ��
��
��PM��![]() ��
��
��P��4����![]() ����
����
����ͼ3�У���AB��AP������BAP����90��ʱ����OB��m��OA��2m��
����AOB�ա�P��NA���ɵ�AN��OB��m��P��N��OA��2m��
��ON��4��2m��m��
��m��4��
��P��N��8��
��P����4��8����
����ͼ3�У���AB��PB����ABP��90��ʱ��ͬ���ɵ�P��4����12����
�������������������ĵ�P����Ϊ��4����![]() ����4��8����4����12����
����4��8����4����12����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�