题目内容
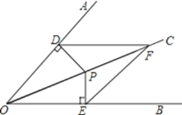
【题目】如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.F是OC上另一点,连接DF,EF.求证:DF=EF.
【答案】详见解析
【解析】
根据角平分线的性质可得出PD=PE,结合OP=OP可证出Rt△POD≌Rt△POE(HL),根据全等三角形的性质可得出OD=OE,结合∠DOF=∠EOF、OF=OF可证出△ODF≌△OEF(SAS),再利用全等三角形的性质即可证出DF=EF.
∵OC是∠AOB的角平分线,P是OC上一点,PD⊥OA,PE⊥OB,
∴∠DOP=∠EOP,PD=PE.
在Rt△POD和Rt△POE中,![]() ,
,
∴Rt△POD≌Rt△POE(HL),
∴OD=OE,
在△ODF和△OEF中, ,
,
∴△ODF≌△OEF(SAS),
∴DF=EF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】如图1是2019年11月的日历,用如图2所示的曲尺形框框(有三个方向,从左往右依次记为一、二、三个框) ,可以框住日历中的三个数,设被框住的三个数中最大的数为![]()
日 | 一 | 二 | 三 | 四 | 五 | 六 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

![]() 请用含
请用含![]() 的代数式填写以下三个空:第一个框框住的最小的数是_ ,第二个框框住的最小的数是__ ,第三个框框住的三个数的和是_ _.
的代数式填写以下三个空:第一个框框住的最小的数是_ ,第二个框框住的最小的数是__ ,第三个框框住的三个数的和是_ _.
![]() 这三个框分别框住的中间的数之和能恰好是
这三个框分别框住的中间的数之和能恰好是![]() 的倍数吗?如能请求出
的倍数吗?如能请求出![]() 的值,若不能请说明理由.
的值,若不能请说明理由.