题目内容
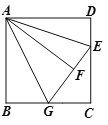
【题目】如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为______.
【答案】![]()
【解析】
先根据正方形的性质可得AD=AB=BC=CD,∠D=∠B=∠BCD=90°,再根据折叠的性质可得AD=AF,DE=EF,∠D=∠AFE=90°,再证明△ABG≌△AFG可得FG=GB,然后设BG=x,则CG=12-x,GE=x+4,再利用勾股定理算出x的值,进而运用勾股定理可得到AG的长.
解:在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
在Rt△ABG和Rt△AFG中,
![]()
∴△ABG≌△AFG(HL),
∴FG=GB,
∵CE=2DE,AB=3,
∴DE=1,CE=2,
设BG=x,则CG=3-x,GE=x+1,
∵GE2=CG2+CE2
∴(x+1)2=(3-x)2+22,
解得![]() ,
,
![]() ,
,
![]() 中
中![]() ,
,
故答案为:![]() .
.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
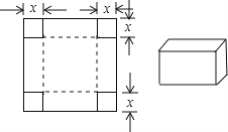
【题目】如图所示,一张边长为16cm的正方形硬纸板,把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
(1)用含有x的代数式表示V,则V=______;
(2)完成下表:
x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
V(cm2) |
(3)观察上表,容积V的值是否随x的增大而增大?当x取什么值时,容积V的值最大?