题目内容
【题目】对于△ABC及其边上的点P,给出如下定义:如果点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 都在△ABC的边上,且
都在△ABC的边上,且![]() ,那么称点
,那么称点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距点,线段
为△ABC关于点P的等距点,线段![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距线段.
为△ABC关于点P的等距线段.
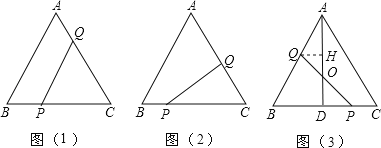
(1)如图1,△ABC中,∠A<90°,AB=AC,点P是BC的中点.

①点B,C △ABC关于点P的等距点,线段PA,PB △ABC关于点P的等距线段;(填“是”或“不是”)
②△ABC关于点P的两个等距点![]() ,
,![]() 分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段
分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段![]() ,
,![]() ;
;
(2)△ABC是边长为4的等边三角形,点P在BC上,点C,D是△ABC关于点P的等距点,且PC=1,求线段DC的长;
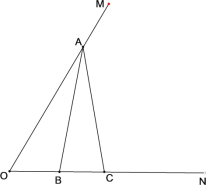
(3)如图2,在Rt△ABC中,∠C=90°,∠B=30°.点P在BC上,△ABC关于点P的等距点恰好有四个,且其中一个是点![]() .若
.若![]() ,直接写出
,直接写出![]() 长的取值范围.(用含
长的取值范围.(用含![]() 的式子表示)
的式子表示)

【答案】(1)①是,不是;②见解析;(2)DC=1或2;(3)![]() .
.
【解析】
(1)①根据阅读材料中△ABC关于点P的等距点和△ABC关于点P的等距线段的定义判断即可;
②根据题意,点P在∠BAC的平分线上,要使相应的等距线段最短,只要过点P作AB、AC的垂线段即可;
(2)显然点D不可能在AB边上,分点D在等边△ABC的边AC、BC上,画出图形,然后根据等距点的概念和等边三角形的判定与性质求解即可;
(3)先求出△ABC关于点P的等距点恰好有3个,且其中一个是点![]() 时的PC的长,进而可得答案.
时的PC的长,进而可得答案.
解:(1)①∵点P是BC的中点,∴PB=PC,∴点B、C是△ABC关于点P的等距点;
∵PA≠PB,∴线段PA,PB不是△ABC关于点P的等距线段;
故答案为:是,不是;
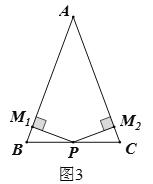
②线段![]() ,
,![]() 如图3所示:
如图3所示:
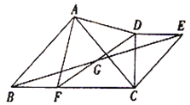
(2)显然,点D不可能在AB边上,若点D在AC边上,如图4所示,
∵△ABC是等边三角形,∴∠C=60°,
∵点C,D是△ABC关于点P的等距点,∴PC=PD,
∴△PCD是等边三角形,∴CD=PC=1;
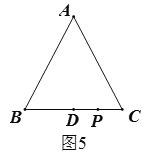
若点D在BC边上,如图5所示,∵点C,D是△ABC关于点P的等距点,∴PC=PD=1,∴CD=2;
∴DC=1或2;
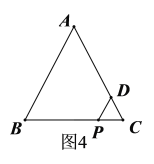
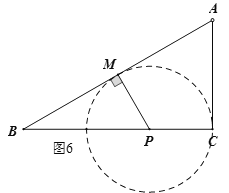
(3)当PM⊥AB且PM=PC时,如图6,此时△ABC关于点P的等距点恰好有3个,且其中一个是点![]() ,
,
∵∠B=30°,∴BP=2PM,∴BC=3PC=a,∴![]() ;
;
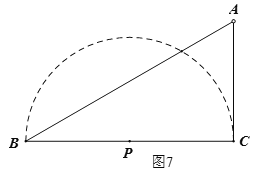
当点P为BC的中点时,如图7所示,此时△ABC关于点P的等距点恰好有3个,且其中一个是点![]() ,∴
,∴![]() ;
;
∴△ABC关于点P的等距点恰好有四个,且其中一个是点![]() 时,PC长的取值范围是:
时,PC长的取值范围是:![]() .
.

 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案