题目内容
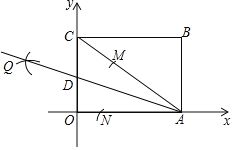
【题目】如图，四边形OABC为矩形，点A，C分别在x轴和y轴上，连接AC，点B的坐标为（8，6），以A为圆心，任意长为半径画弧，分别交AC、AO于点M、N，再分别以M、N为圆心，大于
MN长为半径画弧两弧交于点Q，作射线AQ交y轴于点D，则点D的坐标为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
过点D作DE⊥AC于点E，由勾股定理可求AC=10，由“AAS”可证△ADO≌△ADE，可证AE=AO=8，OD=DE，可得CE=2，由勾股定理可求OD的长，即可求点D坐标．
解：如图，过点D作DE⊥AC于点E，
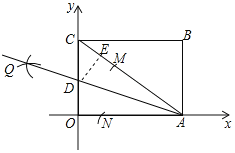
∵四边形OABC为矩形，点B的坐标为（8，6），
∴OA=8，OC=6
∴AC=
=10
由题意可得AD平分∠OAC
∴∠DAE=∠DAO，AD=AD，∠AOD=∠AED=90°
∴△ADO≌△ADE（AAS）
∴AE=AO=8，OD=DE
∴CE=2，
∵CD2=DE2+CE2，
∴（6-OD）2=4+OD2，
∴OD=
∴点D（0，）
故选：B．
练习册系列答案
相关题目
