题目内容
【题目】抛物线y=(a2+1)x2+bx+c经过点A(﹣3,t)、B(4,t)两点,则不等式(a2+1)(x-2)2+bx<2b-c+t的解集是_____________________.
【答案】-1<x<6
【解析】
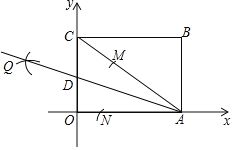
现将(a2+1)(x-2)2+bx<2b-c+t变形(a2+1)(x-2)2+(x-2)b+c<t,即将y=(a2+1)x2+bx+c的图像向右平移2个单位,即y=(a2+1)(x-2)2+(x-2)b+c一定过(﹣1,t)、B(6,t),再由a2+1>0,画出该函数的草图即可确定答案.
解:∵(a2+1)(x-2)2+bx<2b-c+t
∴(a2+1)(x-2)2+(x-2)b+c<t
∵y=(a2+1)(x-2)2+(x-2)b+c的图像可由y=(a2+1)x2+bx+c的图像向右平移2个单位得到
∴y=(a2+1)(x-2)2+(x-2)b+c一定过(﹣1,t)、B(6,t),
又∵a2+1>0,
∴y=(a2+1)(x-2)2+(x-2)b+c的草图如下:
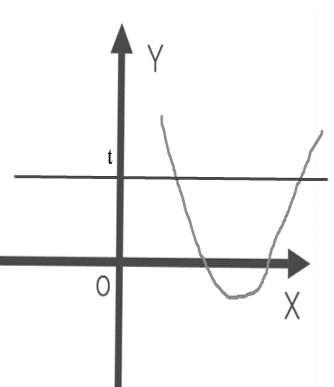
∴(a2+1)(x-2)2+bx<2b-c+t的解集为-1<x<6
故答案为-1<x<6

 阅读快车系列答案
阅读快车系列答案【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?