题目内容
【题目】已知,∠AOD=160°,OB、OM、ON 是∠AOD内的射线
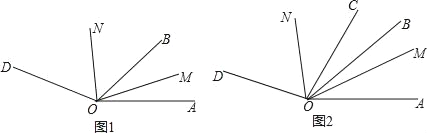
(1)如图1,若OM平分∠AOB,ON平分∠BOD,则∠MON= °
(2)如图2,OC是∠AOD内的射线,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD,当射线OB在∠AOC内时,求∠MON的大小;
(3)如图2,在(2)的条件下,当∠AOB=2t°时,∠AOM:∠DON=2:3,求t的值.
【答案】(1)80(2)70°(3)26
【解析】试题分析:(1)根据角平分线的性质,结合角的和差关系求解即可;
(2)根据题意,设∠AOB=x,则∠BOD=160°﹣x,然后根据角平分线的性质,结合角的和差关系求解即可;
(3)根据由∠AOB=2t°,∠BOC=20°,则∠AOC=2t°+20°,∠BOD=160°﹣2t°,然后根据比例关系列式求解即可.
试题解析:(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=∠BOM+∠BON=![]() (∠AOB+∠BOD),
(∠AOB+∠BOD),
∵∠AOD=∠AOB+∠BOD=160°,
∴∠MON=![]() ×160°=80°;
×160°=80°;
故答案为:80;
(2)设∠AOB=x,则∠BOD=160°﹣x,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=![]() ∠AOC=
∠AOC=![]() (x+20°),∠BON=
(x+20°),∠BON=![]() ∠BOD=
∠BOD=![]() (160°﹣x),
(160°﹣x),
∴∠MON=∠COM+∠BON﹣∠BOC=![]() (x+20°)+
(x+20°)+![]() (160°﹣x)﹣20°=70°;
(160°﹣x)﹣20°=70°;
(3)由∠AOB=2t°,∠BOC=20°,则∠AOC=2t°+20°,∠BOD=160°﹣2t°,
∴∠AOM=![]() ∠AOC=t°+10°,∠DON=
∠AOC=t°+10°,∠DON=![]() ∠BOD=80°﹣t°,
∠BOD=80°﹣t°,
∵∠AOM:∠DON=2:3,
∴![]() =
=![]() ,
,
解得:t=26.

练习册系列答案
相关题目