题目内容
【题目】在△ABC中∠C=90°,D,E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( ) 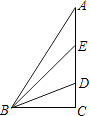
A.BC是△ABE的高
B.BE是△ABD的中线
C.BD是△EBC的角平分线
D.∠ABE=∠EBD=∠DBC
【答案】D
【解析】解:A、BC是△ABE的高,正确,不符合题意;
B、BE是△ABD的中线,正确,不符合题意;
C、BD是△EBC的角平分线,正确,不符合题意;
D、∵BD是△EBC的角平分线,
∴∠EBD=∠DBC,
∵BE是中线,
∴∠ABE≠∠EBD,
∴∠ABE=∠EBD=∠DBC不正确,符合题意.
故选D.
【考点精析】利用三角形的“三线”对题目进行判断即可得到答案,需要熟知1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内.

练习册系列答案
相关题目