题目内容
【题目】如图,△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于F,交AB于E,BF=5cm,求CF的长. 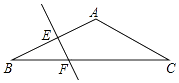
【答案】解:连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF为AB的垂直平分线,
∴AF=BF,
∴∠BAF=∠B=30°,
∴∠FAC=90°,
∵BF=5cm,
∴AF=5cm,
∴FC=10cm.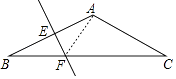
【解析】根据等边对等角可得∠B=∠C=30°,再根据线段垂直平分线的性质可得∠BAF=∠B=30°,进而可得∠FAC=90°,再根据在直角三角形中,30°角所对的直角边等于斜边的一半可得答案.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目