题目内容
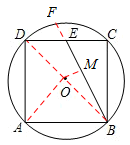
如图,正方形ABCD内接于半径为 的⊙O,E为DC的中点,连接BE,则点O到BE的距离等于 .
的⊙O,E为DC的中点,连接BE,则点O到BE的距离等于 .

 的⊙O,E为DC的中点,连接BE,则点O到BE的距离等于 .
的⊙O,E为DC的中点,连接BE,则点O到BE的距离等于 .
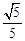 .
.试题分析:连接BD,AO,延长BE交⊙O于点F,作OM⊥BE,
∵正方形ABCD内接于⊙O,∴∠AOD=
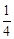 ×360°=90°.
×360°=90°.在△AOD中,由勾股定理得:
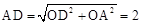 ,∴CD=AD=BC=2.
,∴CD=AD=BC=2.∵E是CD中点,∴DE=CE=1.
在△BCE中,由勾股定理得:BE
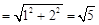 ,
,由相交弦定理得:CE×DE=BE×EF,即1×1=
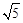 EF,∴EF=
EF,∴EF=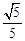 .∴BF=
.∴BF=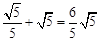 .
.∵OM⊥BF,OM过圆心O,∴BM=FM=
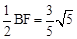 ,
,在△BOM中,由勾股定理得:OB2=OM2+BM2,即
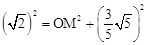 ,解得:OM=
,解得:OM=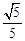 .
.∴点O到 BE的距离等于
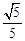 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 ,∠AOB=122°,则∠AOC的度数为( )
,∠AOB=122°,则∠AOC的度数为( )

