题目内容
【题目】在同一平面直角坐标系中，函数
（
）与
的图象可能是（ ）
A.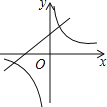
B.
C.
D.
【答案】C
【解析】
根据函数
（
）与
的图象性质，对各选项图像的象限进行判断分析.
解：A图像错误，反比例函数a>0,则一次函数b=-a<0,直线与y轴交点应在x轴下方，
B图像错误，题干可知反比例函数图像在一三象限则有k=a>0,若k=a>0，那么一次函数的一次项系数a也是大于0，常数项-a小于0，直线应在一、三、四象限，
C图像正确，双曲线在二、四象限时，反比例函数k值小于0,则一次函数k值小于0，b=-a>0,直线在一、二、四象限，
D图像错误，双曲线在二、四象限时，反比例函数k值小于0, 则一次函数k值应小于0，b=-a>0，与y轴交点在x轴上方，直线在一、二、四象限，
故答案选C.
练习册系列答案
阅读快车系列答案
相关题目
【题目】如图，某商场设立了一个可以自由转动的转盘，并规定：顾客购物
元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．表是活动进行中的一组统计数据：
计算并完成表格：
转动转盘的次数 |
|
|
|
|
|
|
落在“铅笔”的次数 |
|
|
|
|
|
|
落在“铅笔”的频率 | ________ | ________ | ________ | ________ | ________ | ________ |
请估计，当
很大时，频率将会接近多少？
假如你去转动转盘一次，你获得可乐的概率是多少？
