题目内容
 如图在△ABC中,DE∥AB,FD∥BC,EF∥AC,则下列说法中正确的有( )个.
如图在△ABC中,DE∥AB,FD∥BC,EF∥AC,则下列说法中正确的有( )个.①图中共有三个平行四边形;
②AF=BF,CE=BE,AD=CD;
③EF=DE=DF;
④图中共有三对全等三角形.
分析:①由根据“有一组对边平行且相等的四边形是平行四边形”得到3个平行四边形.然后根据平行四边形的性质和全等三角形的判定定理进行判断.
②利用①中的平行四边形的对边相等的性质进行证明;
③由②中的结论,利用三角形中位线定理来判定;
④根据③的结论知,当△ABC是等边三角形时,图中采用3对全等三角形.
②利用①中的平行四边形的对边相等的性质进行证明;
③由②中的结论,利用三角形中位线定理来判定;
④根据③的结论知,当△ABC是等边三角形时,图中采用3对全等三角形.
解答:解:①如图,∵DE∥AB,FD∥BC,即DE∥BF,FD∥BE,
∴四边形FBED是平行四边形.
同理证得,四边形AFED和四边形FDCE是平行四边形.
综上所述,图中共有三个平行四边形.
故①正确;
②∵在?AFDE中,AF=DE;在?BFDE中,BF=DE,
∴AF=BF.
同理证得,CE=BE,AD=CD.故②正确;
③由②知,点D、E分别是AC、BC边上的中点,
∴ED是该三角形的中位线,
∴ED=
AB.
同理EF=
AC,FD=
BC,
只有当AC=AB=BC时,EF=DE=DF.故③不一定正确;
④当△ABC是等边三角形时,图中有三对全等三角形.故④不一定正确.
综上所述.正确的结论有①②,共2个.
故选B.
∴四边形FBED是平行四边形.
同理证得,四边形AFED和四边形FDCE是平行四边形.
综上所述,图中共有三个平行四边形.
故①正确;
②∵在?AFDE中,AF=DE;在?BFDE中,BF=DE,
∴AF=BF.
同理证得,CE=BE,AD=CD.故②正确;
③由②知,点D、E分别是AC、BC边上的中点,
∴ED是该三角形的中位线,
∴ED=
| 1 |
| 2 |
同理EF=
| 1 |
| 2 |
| 1 |
| 2 |
只有当AC=AB=BC时,EF=DE=DF.故③不一定正确;
④当△ABC是等边三角形时,图中有三对全等三角形.故④不一定正确.
综上所述.正确的结论有①②,共2个.
故选B.
点评:本题主要考查了平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目

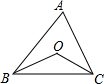 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE, 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是