Question

【题目】△ABC中，AB＝AC，∠A为锐角，CD为AB边上的高，I为△ACD的内切圆圆心，则∠AIB的度数是（ ）

A. 120°B. 125°C. 135°D. 150°

Answer 1

【答案】C

【解析】

CD是AB边上的高，则∠ADC=90°，I是△ACD的内心，则AI、CI分别是∠DAC和∠DCA的角平分线，由此可求得∠AIC的度数；再根据∠AIB和∠AIC的关系，得出∠AIB．

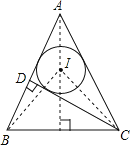
解：如图．∵CD为AB边上的高，

∴∠ADC=90°，

∴∠BAC+∠ACD=90°；

又∵I为△ACD的内切圆圆心，

∴AI、CI分别是∠BAC和∠ACD的角平分线，

∴∠IAC+∠ICA=45°，

∴∠AIC=135°；

又∵AB=AC，∠BAI=∠CAI，AI=AI；

∴△AIB≌△AIC（SAS），

∴∠AIB=∠AIC=135°．

故选C．