题目内容
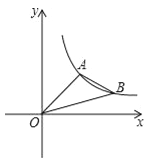
【题目】已知,如图抛物线y=ax2+bx+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点A的坐标为(﹣4,0),B的坐标为(1,0),且OC=4OB.
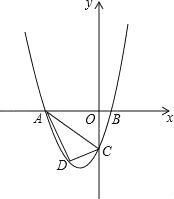
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求三角形ACD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
【答案】(1)y=x2+3x﹣4;(2)三角形ACD面积的最大值=8;(3)存在3个点符合题意,坐标分别是P1(﹣3,﹣4),P2(![]() ,4)和P3(
,4)和P3(![]() ,4).
,4).
【解析】
(1)根据点B的坐标为(1,0),OC=4OB可得出C点坐标,再把A,B,C三点的坐标代入抛物线的解析式求出a,b,c的值即可;
(2)过点D作DM∥y轴分别交线段AC和x轴于点M,N,利用待定系数法求出直线AC的解析式,故可得出DM=(x+2)2+4,即可得出结论;
(3)①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,根据PC两点的纵坐标相等可得出P点坐标;②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,令P(x,4),由x2+3x4=4得出x的值即可得出P点坐标.
解:(1)∵OC=4OB,B(1,0),
∴C(0,﹣4),
把点A,B,C的坐标代入y=ax2+bx+c,得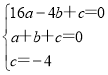
解得: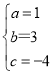 ,
,
∴抛物线线的解析式为:y=x2+3x﹣4;
(2)如图1,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
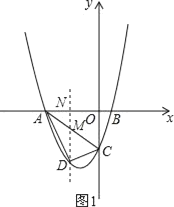
∵A(﹣4,0),B的坐标为(1,0),
∴AB=5,
∴S△ACD=![]() DM×(AN+ON)=
DM×(AN+ON)=![]() DMOA=2DM,
DMOA=2DM,
设直线AC的解析式为y=kx+b(k≠0),
∵A(﹣4,0),C(0,﹣4),
∴![]() ,解得
,解得![]() ,
,
故直线AC的解析式为:y=﹣x﹣4.
令D(x,x2+3x﹣4),M(x,﹣x﹣4),则DM=﹣x﹣4﹣(x2+3x﹣4)=﹣(x+2)2+4,
当x=﹣2时,DM有最大值4,
故三角形ACD面积的最大值=![]() ×4×4=8;
×4×4=8;
(3)①如图2,过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形.
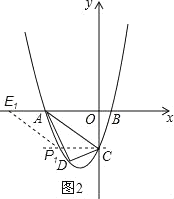
∵C(0,﹣4),令x2+3x﹣4=﹣4,
∴x=0或x=﹣3.
∴P1(﹣3,﹣4).
②如图3,平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
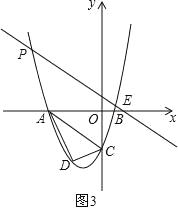
∵C(0,﹣4),
∴可令P(x,4),由x2+3x﹣4=4,得x2+3x﹣8=0.
解得x=![]() 或x=
或x=![]() .
.
此时存在点P2(![]() ,4)和P3(
,4)和P3(![]() ,4).
,4).
综上所述,存在3个点符合题意,坐标分别是P1(﹣3,﹣4),P2(![]() ,4)和P3(
,4)和P3(![]() ,4).
,4).