题目内容
【题目】小明在学习三角形的知识时, 发现如下三个有趣的结论:
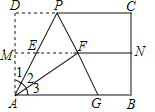
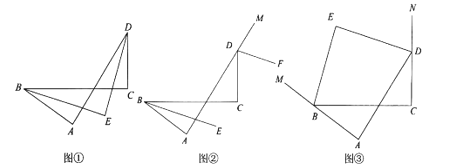
(1)如图①, ∠A=∠C=90°, ∠ABC的平分线与∠ADC的平分线交于点E, 则BE、DE的位置关系是 ;
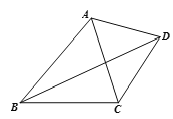
(2)如图②, ∠A=∠C=90°, BE平分∠ABC, DF平分∠ADC的外角, 则BE与DF的位置关系是 ;
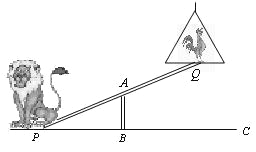
(3)如图③, ∠A=∠C=90°, ∠ABC的外角平分线与∠ADC的外角平分线交于点E, 则BE、DE的位置关系是 . 请你完成命题 (3)证明.
【答案】(1)BE⊥DE; (2)BE//DF; (3)BE⊥DE.证明见解析.
【解析】
(1)由∠A=∠C=90°可以得到∠HDC=∠ABH,设∠HDC=∠ABH=x,可得∠HDG=∠CDG=∠FBH=∠ABF=![]() x,则有∠CDG+∠CGD=90°,由∠CGD=∠BGE,可得∠BGE+∠FBE=90°,即BE⊥DE;
x,则有∠CDG+∠CGD=90°,由∠CGD=∠BGE,可得∠BGE+∠FBE=90°,即BE⊥DE;
(2) 由∠A=∠C=90°可以得到∠HDC=∠ABH,设∠HDC=∠ABH=x,可得∠EBH=∠ABE=![]() x,则∠DGE=90°+
x,则∠DGE=90°+![]() x,∠CDM=180°-x,由DF平分∠CDM,则∠CDF=
x,∠CDM=180°-x,由DF平分∠CDM,则∠CDF=![]() (180°-x),所以∠CDF+∠HDC=
(180°-x),所以∠CDF+∠HDC=![]() (180°-x),然后运用同位角相等,即可证明;
(180°-x),然后运用同位角相等,即可证明;
(3)设∠BFA=∠CFD=x,由∠A=∠C=90°可以得到∠EBC=∠FDN=90°+x,由根据题意可得:∠EDF=∠EBF=![]() (90°+x);且∠BFD=180°+x,最后用四边形内角和,求出∠BED=90°,完成证明.
(90°+x);且∠BFD=180°+x,最后用四边形内角和,求出∠BED=90°,完成证明.

解:(1)BE⊥DE,理由如下:
∵∠A=∠C=90°,∠DHC=∠BHA
∴∠HDC=∠ABH
设∠HDC=∠ABH=x
∵∠ABC的平分线与∠ADC的平分线交于点E
∴∠HDG=∠CDG=∠FBH=∠ABF=![]() x
x
又∵∠CDG+∠CGD=90°,∠CGD=∠BGE
∴∠BGE+∠FBE=90°,即BE⊥DE;
(2)

DF∥AB,理由如下:
∵∠A=∠C=90°,∠DHC=∠BHA
∴∠HDC=∠ABH
∵∠A=∠C=90°,∠DHC=∠BHA
∴∠HDC=∠ABH
∵BE平分∠ABH,
∴∠EBH=∠ABE=![]() x
x
∴∠DGE=90°+![]() x
x
∵∠CDM=180°-x,DF平分∠CDM
∴∠CDF=![]() (180°-x)=90°-
(180°-x)=90°-![]() x
x
∴∠HDF=∠CDF+∠CDH=90°-![]() x+x=90°+
x+x=90°+![]() x
x
∴∠DGE=∠HDF
∴DF∥AB
(3)

BE⊥DE,证明如下:
设∠BFA=∠CFD=x,
∵∠A=∠C=90°
∴∠EBC=∠FDN=90°+x,
∵∠ABC的外角平分线与∠ADC的外角平分线交于点E
∴∠EDF=∠EBF=![]() (90°+x)
(90°+x)
又∵∠BFD=180°-∠AFB=180°-x
∴∠BFD=360°-![]() (90°+x)-
(90°+x)-![]() (90°+x)-(180°-x)=90°
(90°+x)-(180°-x)=90°
即BE⊥DE

 字词句段篇系列答案
字词句段篇系列答案