题目内容
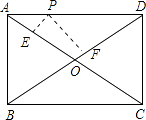
【题目】如图,对折矩形纸片ABCD,使AB与DC重合,得到折痕MN,将纸片展平;再一次折叠,使点D落到MN上的点F处,折痕AP交MN于E;延长PF交AB于G.求证:
(1)△AFG≌△AFP;
(2)△APG为等边三角形.
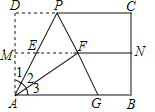
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由折叠的性质得到M、N分别为AD、BC的中点,利用平行线分线段成比例得到F为PG的中点,再由折叠的性质得到AF垂直于PG,利用SAS即可得证;
(2)由(1)的全等三角形,得到对应边相等,利用三线合一得到∠2=∠3,由折叠的性质及等量代换得到∠PAG为60°,根据AP=AG且有一个角为60°即可得证.
(1)由折叠可得:M、N分别为AD、BC的中点,
∵DC∥MN∥AB,
∴F为PG的中点,即PF=GF,
由折叠可得:∠PFA=∠D=90°,∠1=∠2,
在△AFP和△AFG中,
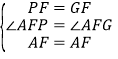 ,
,
∴△AFP≌△AFG(SAS);
(2)∵△AFP≌△AFG,
∴AP=AG,
∵AF⊥PG,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠2=∠3=30°,
∴∠2+∠3=60°,即∠PAG=60°,
∴△APG为等边三角形.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目