题目内容
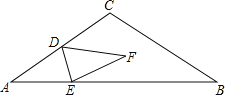
【题目】如图,在等腰三角形ABC中,AC=BC=4,∠A=30°,点D为AC的中点,点E为边AB上一个动点,连接DE,将△ADE沿直线DE折叠,点A落在点F处.当直线EF与直线AC垂直时,则AE的长为_____.
【答案】![]() 或
或![]()
【解析】
当直线EF与直线AC垂直时,如图1,如图2,根据折叠的性质得到和等腰三角形的判定和性质定理以及直角三角形的性质健康得到结论.
解:∵AC=4,点D为AC的中点,
∴AD=![]() AC=2,
AC=2,
①当直线EF与直线AC垂直时,如图1,
∵将△ADE沿直线DE折叠,点A落在点F处,
∴∠F=∠A=30°,∠AED=∠FED,
∵∠AGE=90°,
∴∠AEG=60°,
∴∠AED=∠FED=30°,
∴AD=DE=2,
过D作DM⊥AE与M,
∴AE=2AM=2×![]() ×2=2
×2=2![]() ;
;
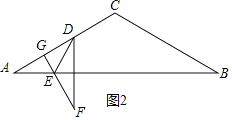
当直线EF与直线AC垂直时,如图2,
∵将△ADE沿直线DE折叠,点A落在点F处,
∴∠F=∠A=30°,∠ADE=∠FDE,
∵∠AGE=∠FGE=90°,
∴∠FGD=60°,
∴∠ADE=∠FDE=30°,
∴∠A=∠ADE,
∴AE=DE,
∴AG=![]() AD=1,
AD=1,
∴AE=![]() ,
,
综上所述,![]() 或
或![]()
故答案为:![]() 或2
或2![]() .
.


练习册系列答案
相关题目
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率