题目内容
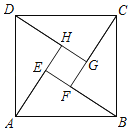
【题目】某公司对办公大楼一块墙面进行如图所示的图案设计．这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形，设小正方形的边长m，直角三角形较短边长n，且n＝2m﹣4，大正方形的面积为S．
（1）求S关于m的函数关系式．
（2）若小正方形边长不大于3，当大正方形面积最大时，求m的值．
【答案】（1）S＝13m2﹣40m+32（m＞2）；（2）m＝3
【解析】
（1）根据小正方形的边长m，直角三角形较短边长n，即可得出直角三角形较长边长为m+n，根据勾股定理即可得出函数关系式；
（2）根据二次函数的性质和题意中的取值范围即可得出S的最大值，从而可求的m．
解：（1）∵小正方形的边长m，直角三角形较短边长n，
∴直角三角形较长边长为m+n，
∴由勾股定理得：S＝（m+n）2+n2，
∵n＝2m﹣4，
∴S＝（m+2m﹣4）2+（2m﹣4）2，
＝13m2﹣40m+32，
∵n＝2m﹣4＞0，
∴m＞2，
∴S关于m的函数关系式为S＝13m2﹣40m+32（m＞2）；
（2）∵S＝13m2﹣40m+32（2＜m≤3），
∴S＝13(m-
)2+
∵m≥时，S随x的增大而增大，
∴m＝3时，S取最大．
∴m＝3．
练习册系列答案
相关题目
