Question

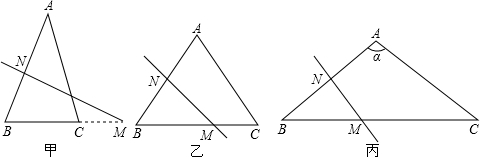
如图甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．

解答下列问题：

（1）如果AB=AC，∠BAC=90º．

①当点D在线段BC上时（与点B不重合），如图乙，线段CF、BD之间的位置关系为        ，数量关系为        ．

②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？

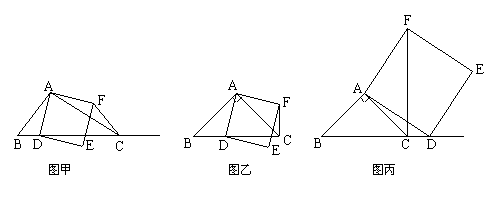
（2）如果AB≠AC，∠BAC≠90º，点D在线段BC上运动．

试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外

画出相应图形，并说明理由．（画图不写作法）

（3）若AC＝，BC=3，在（2）的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值．

Answer 1

（1） ①CF与BD位置关系是 垂 直、数量关系是 相 等；

②当点D在BC的延长线上时①的结论仍成立．

由正方形ADEF得 AD=AF ，∠DAF=90º．

∵∠BAC=90º，∴∠DAF=∠BAC ， ∴∠DAB=∠FAC，

又AB=AC ，∴△DAB≌△FAC ， ∴CF=BD　 ∠ACF=∠ABD．

∵∠BAC=90º， AB=AC ，∴∠ABC=45º，∴∠ACF=45º，

∴∠BCF=∠ACB+∠ACF= 90º．即 CF⊥BD　

（2）画图正确　　　　　　　当∠BCA=45º时，CF⊥BD（如图丁）

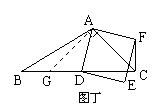理由是：过点A作AG⊥AC交BC于点G，∴AC=AG

可证：△GAD≌△CAF　 ∴∠ACF=∠AGD=45º

∠BCF=∠ACB+∠ACF= 90º．　 即CF⊥BD）

（3）当具备∠BCA=45º时，

过点A作AQ⊥BC交BC的延长线于点Q，（如图戊）

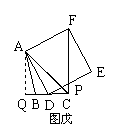∵DE与CF交于点P时， ∴此时点D位于线段CQ上，

∵∠BCA=45º，可求出AQ= CQ=4．设CD=x ，∴ DQ=4—x，

容易说明△AQD∽△DCP，∴ ， ∴，

．

∵0＜x≤3　 ∴当x=2时，CP有最大值1．