题目内容
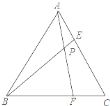
【题目】公园内一凉亭，凉亭顶部是一圆锥形的顶盖，立柱垂直于地面，在凉亭内中央位置有一圆形石桌，某数学研究性学习小组，将此凉亭作为研究对象，并绘制截面示意图，其中顶盖母线AB与AC的夹角为124°，凉亭顶盖边缘B、C到地面的距离为2.4米，石桌的高度DE为0.6米，经观测发现：当太阳光线与地面的夹角为42°时，恰好能够照到石桌的中央E处（A、E、D三点在一条直线上），请你求出圆锥形顶盖母线AB的长度．（结果精确到0.1m）（参考数据：sin62°≈0.88，tan42°≈0.90）
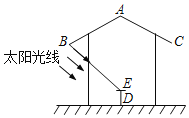
【答案】2.3米
【解析】
连接BC、AE，交于点O，则AE⊥BC．解Rt△OBD，求出OB=
≈
＝2．解Rt△OAB中，即可求出AB=
．
如图，连接BC、AE，交于点O，则AE⊥BC．
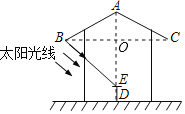
由题意，可知OE＝2.4﹣0.6＝1.8，∠OBE＝42°，∠BAO＝
∠BAC＝62°．
在Rt△OBD中，∵tan∠OBE＝
，
∴OB＝≈＝2．
在Rt△OAB中，∵sin∠OAB＝
，
∴AB＝≈
≈2.3（m）．
答：圆锥形顶盖母线AB的长度约为2.3米．
练习册系列答案
相关题目
