Question

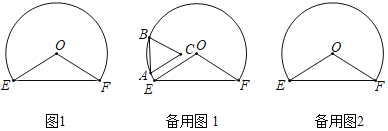
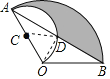
【题目】如图，在扇形AOB中，∠AOB＝120°，连接AB，以OA为直径作半圆C交AB于点D，若OA＝4，则阴影部分的面积为_____．

Answer 1

【答案】4π﹣3

【解析】

连接OD、CD，根据圆周角定理得到OD⊥AB，根据等腰三角形的性质得到AD=DB，∠OAD=30°，根据扇形面积公式、三角形的面积公式计算即可．

解：连接OD、CD，

∵OA为圆C的直径，

∴OD⊥AB，

∵OA＝OB，∠AOB＝120°，

∴AD＝DB，∠OAD＝30°，

∴OD＝OA＝2，

由勾股定理得，AD＝,

∴△AOB的面积＝×AB×OD＝4，

∵OC＝CA，BD＝DA，

∴CD∥OB，CD＝OB，

∴∠ACD＝∠AOB＝120°，△ACD的面积＝×△AOB的面积＝，

∴阴影部分的面积＝﹣△AOB的面积﹣（﹣△ACD的面积）

＝π﹣4﹣π+

＝4π﹣3，

故答案为：4π﹣3．