题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.

![]() 求抛物线的解析式及顶点
求抛物线的解析式及顶点![]() 的坐标;
的坐标;
![]() 判断
判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
![]() 点
点![]() 是
是![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标.
的坐标.
【答案】![]()
![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ;
;![]() 是直角三角形.理由见解析;
是直角三角形.理由见解析;![]()
![]() .
.
【解析】
(1)、将点A的坐标代入解析式得出b的值,从而得出函数解析式,将解析式进行配方得出顶点坐标;(2)、根据函数解析式得出点B和点C的坐标,从而得出AB、AC和BC的长度,从而得出三角形的形状;(3)、作出点C关于x轴的对应点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,利用待定系数法求出直线
,利用待定系数法求出直线![]() 的解析式,从而得出点M的坐标.
的解析式,从而得出点M的坐标.
![]() ∵点
∵点![]() 在抛物线
在抛物线![]() 上,∴
上,∴![]() ,
,
解得![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
∵![]() ,∴顶点
,∴顶点![]() 的坐标为
的坐标为![]() ;
;
![]() 是直角三角形.理由如下:当
是直角三角形.理由如下:当![]() 时,
时,![]() ,∴
,∴![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() ,
,![]() ,则
,则![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() . ∵
. ∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 是直角三角形;
是直角三角形;
![]() 作出点
作出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() .
.
连接![]() 交
交![]() 轴于点
轴于点![]() ,
,
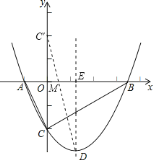
根据轴对称性及两点之间线段最短可知,![]() 一定,当
一定,当![]() 的值最小时,
的值最小时,![]() 的周长最小.
的周长最小.
设直线![]() 的解析式为
的解析式为![]() ,则
,则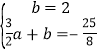 ,解得
,解得![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() ,则
,则![]() , ∴
, ∴![]() .
.

练习册系列答案
相关题目