Question

【题目】如图，在等腰梯形中，，对角线于点，点在轴上，点、在轴上．

若，，求点的坐标；

若，，求过点的反比例函数的解析式；

如图，在上有一点，连接，过作交于，交于，在上取，过作交于，交于，当在上运动时，（不与、重合），的值是否发生变化？若变化，求出变化范围；若不变，求出其值．

Answer 1

【答案】（1）；（2）：；（3）.

【解析】

（1）根据等腰三角形的性质知：AD＝BC，在Rt△AOD中，已知AD，OA的长，可将OD的长求出，从而可知点D的坐标；

（2）作辅助线，作BH⊥DE于H，过B点作BE∥AC交x轴于点E，则四边形ABEC为平行四边形，AB＝CE，BE＝AC，由AC⊥BD，可得：BD⊥BE，故在Rt△BDE中，由斜边DE的长可知：BH的长，在Rt△BHC中，运用勾股定理可将CH的长求出，进而可将OH的长求出，知点B的坐标，从而可求出求过B点的反比例函数的解析式；

（3）作辅助线，过点D作DN∥PC交PE的延长线于点M，交HF的延长线于点N，过点M作MI∥EF交BN于点I，易证四边形EFIM和四边形MNHP是平行四边形，从而可证：△EDM≌△IMN，DM＝MN，进而可证：△PDM≌△CPQ，DM＝PQ＝PH，故：＝1，为定值．

在等腰梯形中，，

又∵，

∴，

∴，

∴；

作于，过点作交轴于点，

∵，，

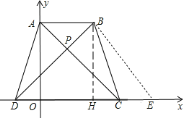
∴是平行四边形，

∴，，

又∵为等腰梯形，

∴，

∴，

而，，

∴，

∵，

∴为的中点，即为直角三角形斜边上的中线，

∴

∵

∴

∴

∴

∴过点的反比例函数的解析式为：；

过点作交的延长线于点，交的延长线于点，过点作交于点，

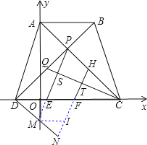
易证四边形和四边形是平行四边形，

∴，，

又∵，，

∴，

∴，

∵，，

∴，.

由知：，而，

∴，

∴，

∴，

∴