题目内容
【题目】如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字。有人为甲、乙两人设计了一个游戏，其规则如下：
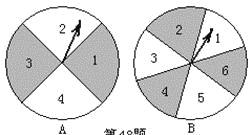
同时自由转动转盘A与B转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针停留在某一数字为止），用所指的两个数字作乘积，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜（如转盘A指针指向3，转盘B指针指向5，3×5＝15，按规则乙胜）。你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由。
【答案】（1）不公平，可能出现的情况为，（1,1）（1,2）（1,3）（1,4）（1,5）（1,6）（2,1）（2,2）（2,3）（2,4）（2,5）（2,6）（3,1）（3,2）（3,3）（3,4）（3,5）（3,6）（4,1）（4,2）（4,3）（4,4）（4,5）（4,6）共有24种等可能的结果，偶数有18种，奇数有6种，甲胜的概率为
，乙胜的概率为
，所以不公平．
（2）可改为用转盘A．B所指的两个数字相加，如果得到的和是偶数，那么甲胜；如果得到的积是奇数，那么乙胜．
【解析】
游戏是否公平，关键要看游戏双方获胜的机会是否相等，即判断双方取胜的概率是否相等，或转化为在总情况明确的情况下，判断双方取胜所包含的情况数目是否相等．
这个游戏不公平，列表如下：
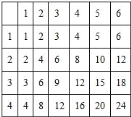
由上表所知总积数共
种，其中积是奇数的有
种，积是偶数的有
种，因此甲获胜的可能性是
，乙获胜的可能性是
．
把游戏中由
，
两个转盘中所指的两个数字的“积”改成“和”，游戏就公平了．因为在盘和盘中指针所指的两个数字作和共有种情况，而盘中每个数字与盘中的各数字作和得到偶数和奇数的种数都是
，所以甲，乙获胜的可能性都为
．
快捷英语周周练系列答案
