题目内容
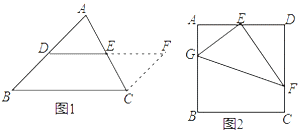
【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若EA=EG,求证:ED=EC.

【答案】见解析
【解析】分析:(1)由条件可先证得四边形ABCF为平行四边形,再由∠B=90°可证得结论;
(2)利用等腰三角形的性质可求得∠EAG=∠EGA=∠FGC,再利用直角三角形的性质可求得∠D=∠ECD,可证得ED=EC.
详解:证明:(1)∵AB∥CD,且FC=AB,
∴四边形ABCF为平行四边形,
∵∠B=90°,
∴四边形ABCF是矩形;
(2)∵EA=EG,
∴∠EAG=∠EGA=∠FGC,
∵四边形ABCF为矩形,
∴∠AFC=∠AFD=90°,
∴∠D+∠DAF=∠FGC+∠ECD=90°,
∴∠D=∠ECD,
∴ED=EC.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?