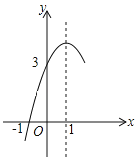题目内容
【题目】如图，平面直角坐标系中，二次函数y=﹣
x2+bx+c的图线与坐标轴分别交于点A、B、C，其中点A（0，8），OB=
OA．
（1）求二次函数的表达式；
（2）若OD=OB，点F为该二次函数在第二象限内图象上的动点，E为DF的中点，当△CEF的面积最大时，求出点E的坐标；
（3）将三角形CEF绕E旋转180°，C点落在M处，若M恰好在该抛物线上，求出此时△CEF的面积．
【答案】（1）y=﹣
x2﹣x+8；（2）E（﹣
，
）；（3）
【解析】分析：（1）根据题意得出B点坐标，进而利用待定系数法求出函数解析式；
（2）首先求出直线DC的解析式进而表示出FP的长，再表示出S△CEF，进而得出E的坐标；
（3）根据题意表示出M点坐标，进而代入二次函数解析式得出m的值，即可得出答案．
详解：（1）∵OA=8，
∴OB=
OA=4，
∴B（4，0），
∵y=﹣x2+bx+c的图象过点A（0，8），B（4，0），
∴
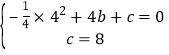，解得：
，
∴二次函数表达式为：y=﹣x2﹣x+8；
（2）当y=0时，﹣x2﹣x+8=0，
解得：x1=4，x2=﹣8，
∴C点坐标为：（﹣8，0），
∵D点坐标为：（0，4），
∴设CD的解析为：y=kx+d，
故
，解得：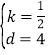
，
故直线DC的解析为：y=x+4；
如图1，过点F作y轴的平行线交DC于点P，
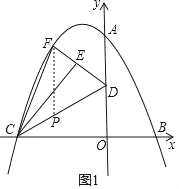
设F点坐标为：（m，﹣m2﹣m+8），则P点坐标为：（m，m+4），
则FP=﹣m2﹣m+4，
∴S△FCD=FPOC=×（﹣m2﹣m+4）×8
=﹣m2﹣6m+16，
∵E为FD中点，
∴S△CEF=×S△FCD=﹣m2﹣3m+8=﹣（m﹣3）2+
，
当m=﹣3时，S△CEF有最大值，
∴﹣m2﹣m+8=﹣×9+3+8=
，
E点纵坐标为：×（﹣4）+4=，
∴F（﹣3，），
∴E（﹣，）；
（3）如图2，∵F点坐标为：（m，﹣m2﹣m+8），
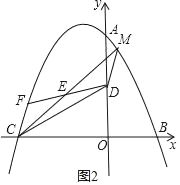
C点坐标为：（﹣8，0），D点坐标为：（0，4），
∴M（m+8，﹣m2﹣m+12），
又∵M点在抛物线上，
∴﹣（m+8）2﹣（m+8）+8=﹣m2﹣m+12，
解得：m=﹣7，
故S△CEF=﹣m2﹣3m+8=．
