题目内容
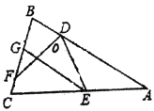
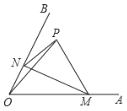
【题目】如图,![]() ,点
,点![]() 是
是![]() 内的定点,且
内的定点,且![]() ,若点
,若点![]() 、
、![]() 分别是射线
分别是射线![]() ,
,![]() 上异于点
上异于点![]() 的动点,则
的动点,则![]() 周长的最小值是______.
周长的最小值是______.
【答案】3
【解析】
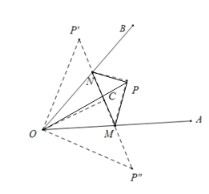
过点P分别作OB、OA的对称点![]() 、
、![]() ,连接
,连接![]() 分别交OB、OA于点N、M,连接O
分别交OB、OA于点N、M,连接O![]() 、O
、O![]() 、PN和PM,过点O作OC⊥
、PN和PM,过点O作OC⊥![]() 于点C,由对称的性质、两点之间线段最短可得此时
于点C,由对称的性质、两点之间线段最短可得此时![]() 即为
即为![]() 的周长的最小值,然后根据30°所对的直角边是斜边的一半和勾股定理即可求出结论.
的周长的最小值,然后根据30°所对的直角边是斜边的一半和勾股定理即可求出结论.
解:过点P分别作OB、OA的对称点![]() 、
、![]() ,连接
,连接![]() 分别交OB、OA于点N、M,连接O
分别交OB、OA于点N、M,连接O![]() 、O
、O![]() 、PN和PM,过点O作OC⊥
、PN和PM,过点O作OC⊥![]() 于点C
于点C
由对称的性质可得:![]() N=PN,
N=PN,![]() M=PM,O
M=PM,O![]() =O
=O![]() =OP=
=OP=![]() ,∠NO
,∠NO![]() =∠NOP,∠MO
=∠NOP,∠MO![]() =∠MOP
=∠MOP
∴△PMN的周长=PN+MN+PM=![]() N+MN+
N+MN+![]() M=
M=![]() ,
,![]() =2
=2![]() ,∠NO
,∠NO![]() +∠MO
+∠MO![]() =∠NOP+∠MOP =∠MON=60°,
=∠NOP+∠MOP =∠MON=60°,
∴根据两点之间线段最短,此时![]() 即为△PMN的周长的最小值,∠
即为△PMN的周长的最小值,∠![]() O
O![]() =∠NO
=∠NO![]() +∠MO
+∠MO![]() +∠MON =120°
+∠MON =120°
∴∠O![]()
![]() =∠O
=∠O![]()
![]() =
=![]() (180°-∠
(180°-∠![]() O
O![]() )=30°
)=30°
∴OC=![]() O
O![]() =
=![]() ,
,![]() =
=![]()
∴![]() =3
=3
即△PMN周长的最小值为3
故答案为:3.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了三项素质测试.各项测试成绩如表格所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
专业知识 | 74 | 87 | 90 |
语言能力 | 58 | 74 | 70 |
综合素质 | 87 | 43 | 50 |
(1)根据实际需要,公司将专业知识、语言能力和综合素质三项测试得分按4:3:1的比例确定每个人的测试总成绩,此时谁将被录用?
(2)请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩,使得乙被录用,若重新设计的比例为x:y:1,且x+y+1=10,则x= ,y= .(写出x与y的一组整数值即可)