题目内容
【题目】已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A出发,沿线段AB向点B运动.
(1)如图1,设点P的运动时间为t(s),那么t为何值时,△PBC是直角三角形;
(2)若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D.如果动点P,Q都以1cm/s的速度同时出发.
①如图2,设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?
②如图3,连接PC,请你猜想:在点P,Q的运动过程中,△PCD和△QCD的面积有什么关系?并说明理由.
【答案】
(1)
解:当△PBC是直角三角形时,∠B=60°,
∠BPC=90°,所以BP=1.5cm,
所以t= ![]()
(2)
解:①∵∠DCQ=120°,
当△DCQ是等腰三角形时,CD=CQ,
∴∠PDA=∠CDQ=∠CQD=30°,
∵∠A=60°,
∴AD=2AP,
∴2t+t=3,
解得t=1(s);
②相等,如图所示:
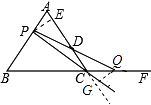
作PE垂直AD,QG垂直AD延长线,则PE∥QG,
∴∠G=∠AEP,
在△EAP和△GCQ, 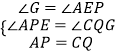 ,
,
∴△EAP≌△GCQ(AAS),
∴PE=QG,
∴△PCD和△QCD同底等高,
所以面积相等
【解析】(1)当△PBC是直角三角形时,∠B=60°,所以BP=1.5cm,即可算出t的值;(2)①因为∠DCQ=120°,当△DCQ是等腰三角形时,CD=CQ,然后可证明△APD是直角三角形,即可根据题意求出t的值;②面积相等.可通过同底等高的三角形的面积相等即可.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)的相关知识才是答题的关键.

练习册系列答案
相关题目


