题目内容
【题目】(1)操作发现如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决(设DF=x,AD=y.)
保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求
保持(1)中条件不变,若DC=nDF,求![]() 的值.
的值.
【答案】(1)同意;理由见解性;(2)![]() ;(3)
;(3)![]()
【解析】
解(1)同意. 连接EF,则∠BEG=∠D=90°,EG=AE=ED,EF=EF.
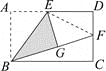
∴Rt△EGF≌Rt△EDF,∴GF=DF.
(2)由(1)知,GF=DF.
设DF=x,BC=y,则有GF=x,AD=y.
∵DC=2DF
∴CF=x,DC=AB=BG=2x.
∴BF=BG+GF=3x.
在Rt△BCF中,BC2+CF2=BP2,即y2+x2=(3x)2.
∴y=2![]() x.
x.
∴![]()
(3)由(1)知GF=DF.
设DF=x,BC=y,则有GF=x,AD=y.
∵DC=n·DF
∴DC=AB =BG=nx.
∴CF=(n-1)x,BF=BG+GF=(n+1)x.
在Rt△BCF中,BC2+CF2=BF2,即y2+[(n-1)x]2=[(n+1)x]2.
∴y=2![]() x.
x.
∴![]() (或
(或![]() )
)

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目