题目内容
【题目】已知,抛物线![]() ,直线
,直线![]() .
.
(1)当![]() 时,求抛物线与
时,求抛物线与![]() 轴交点的坐标;
轴交点的坐标;
(2)直线是否可能经过抛物线的顶点,如果可能,请求出![]() 的值,如果不可能,请说明理由;
的值,如果不可能,请说明理由;
(3)记![]() ,当
,当![]() 时,求
时,求![]() 的最大值.
的最大值.
【答案】(1)抛物线与![]() 轴交点的坐标为
轴交点的坐标为![]() 和
和![]() ;(2)直线不可能经过抛物线的顶点;理由见解析;(3)
;(2)直线不可能经过抛物线的顶点;理由见解析;(3)![]() 的最大值为4.
的最大值为4.
【解析】
(1)令y=0,可求得x的值,即可得出与x轴交点坐标;
(2)将抛物线的顶点代入直线解析式中,解得m=0矛盾,可得直线不经过顶点;
(3)分2种情况讨论,目的是去绝对值,然后根据二次函数的性质分别求最大值,比较得出最终的最大值.
(1)解:当![]() 时,
时,![]()
令![]() ,得
,得![]() .
.
解得![]() ,
,![]()
∴抛物线与![]() 轴交点的坐标为
轴交点的坐标为![]() 和
和![]()
(2) 解:![]()
∴抛物线的顶点为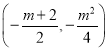
将顶点坐标代入![]() 中,得
中,得
![]()
解得![]()
![]() ,
,
∴直线不可能经过抛物线的顶点.
(3)解:令![]() ,得
,得![]() .
.
当![]() 时,
时,
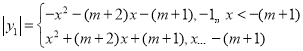 ,
,
![]() .
.
①当![]() ,即
,即![]() 时,
时,
![]()
当![]() 时,
时,![]()
![]() .
.
![]()
②当![]() ,即
,即![]() 时,
时,
![]()
当![]() 时,
时,![]() .
.
![]() ,
,
![]()
综上所述,![]() 的最大值为4.
的最大值为4.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目