题目内容
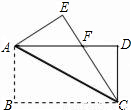
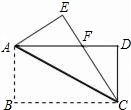
 如图,在长方形ABCD中,点E在BC上,点F在CD上,已知AB=6,AD=5,BE=2,CF=1,连接AE、EF、AF
如图,在长方形ABCD中,点E在BC上,点F在CD上,已知AB=6,AD=5,BE=2,CF=1,连接AE、EF、AF
(1)S△AEF=______(直接填空)
(2)求证:△AEF为直角三角形.
解:(1)∵四边形ABCD是矩形,
∴AB=DC=6,AD=BC=5,
∴DF=DC-CF=4,CE=BC-BE=3,
∴S△AEF=S矩形ABCD-S△ABE-S△FCE-S△ADF=20,
故答案为:20;
(2)∵∠B=90°,AB=6,BE=2,
∴AE2=AB2+BE2=40,
同理可得:EF2=CF2+CE2=10,AF2=AD2+DF2=50,
∴AE2+EF2=AF2,
∴△AEF为直角三角形.
分析:(1)由题意可知S△AEF=S矩形ABCD-S△ABE-S△FCE-S△ADF根据三角形的面积公式在分别计算即可;
(2)根据勾股定理分别计算AE,EF,AF的长,再根据勾股定理的逆定理判定即可.
点评:本题考查了矩形的性质,三角形的面积公式以及勾股定理和其逆定理的运用.
∴AB=DC=6,AD=BC=5,
∴DF=DC-CF=4,CE=BC-BE=3,
∴S△AEF=S矩形ABCD-S△ABE-S△FCE-S△ADF=20,
故答案为:20;
(2)∵∠B=90°,AB=6,BE=2,
∴AE2=AB2+BE2=40,
同理可得:EF2=CF2+CE2=10,AF2=AD2+DF2=50,
∴AE2+EF2=AF2,
∴△AEF为直角三角形.
分析:(1)由题意可知S△AEF=S矩形ABCD-S△ABE-S△FCE-S△ADF根据三角形的面积公式在分别计算即可;
(2)根据勾股定理分别计算AE,EF,AF的长,再根据勾股定理的逆定理判定即可.
点评:本题考查了矩形的性质,三角形的面积公式以及勾股定理和其逆定理的运用.

练习册系列答案
相关题目
 于点F.
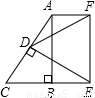
于点F.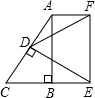 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.