题目内容
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.

【答案】答案见解析
【解析】整体分析:
因为不确定△BPA′的哪一个角是直角,所以需要分三种情况讨论,即(1)当∠BA′P=90°时;(2)当∠A′PB=90°时;(3)当∠A′BP=90°时,注意画出符合各种情况的图形,找出折叠后相等的边和角.
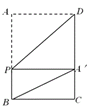
解:(1)当∠BA′P=90°时,由折叠得,∠PA′D=∠A=90°,
∴∠BA′D=∠BA′P+∠PA′D=180°,
∴点B、A′、D在一直线上,
Rt△ABD中,AD=6,AB=8,由勾股定理得BD=10.
设AP=xcm,
∴A′P=x,BP=8-x,A′B=10-6=4,
在Rt△A′PB中,x2+42=(8-x)2,
解得x=3.
∴点P运动的时间为3÷1=3秒.
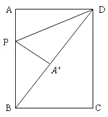
(2)当∠A′PB=90°时,∠A′PA=90°,
∵∠DA′P=90°,∴四边形APA′D是矩形,
∴A′P=AP,∴四边形APA′D是正方形,∴AP=AD=6,
∴点P运动的时间为6÷1=6秒.
(3)当∠A′BP=90°时,不存在.
综上所述,点P的运动时间为3s或6s.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目