题目内容
【题目】在平面直角坐标系中,直线y=-![]() 分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.


(1)填空:b= ;
(2)求点D的坐标;
(3)点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
【答案】(1)6;(2)点D的坐标为(14,8);(3)存在,点N的坐标为(4,3)或(![]() ,
,![]() ).
).
【解析】
(1)把(8,0)代入y=![]() x+b即可求得b的值;
x+b即可求得b的值;
(2)过点D作DE⊥x轴于点E,证明△OAB≌△EDA,即可求得AE和DE的长,则点D的坐标即可求得;
(3)分两种情况讨论:①当OM=MB=BN=NO时,求出点M的坐标即可;②当OB=BN=NM=MO=6时,求出对角线交点的坐标即可.
解:(1)把(8,0)代入y=![]() x+b,得:6+b=0,
x+b,得:6+b=0,
解得:b=6,
故答案是:6;
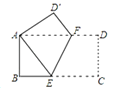
(2)如图1,过点D作DE⊥x轴于点E,
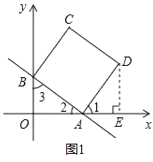
∵在正方形ABCD中,∠BAD=90°,
∴∠1+∠2=90°,
又∵在直角△OAB中,∠2+∠3=90°,
∴∠1=∠3,
在△OAB和△EDA中,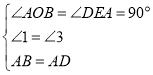 ,
,
∴△OAB≌△EDA(AAS),
∴AE=OB,DE=OA,
∵b=6,点A的坐标为(8,0),
∴AE=OB=6,DE=OA=8,
∴OE=8+6=14,
∴点D的坐标为(14,8);
(3)存在.
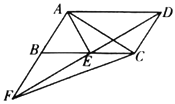
①如图2,当OM=MB=BN=NO时,四边形OMBN为菱形,则MN在OB的中垂线上,即M的纵坐标是3,
把y=3代入y=![]() x+6中,得x=4,即M的坐标是(4,3),
x+6中,得x=4,即M的坐标是(4,3),
则点N的坐标为(4,3);
②如图3,当OB=BN=NM=MO=6时,四边形BOMN为菱形,连接ON交BM于F,
∵ON⊥BM,
∴直线ON的解析式为:y=![]() x,
x,
联立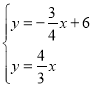 ,解得:
,解得: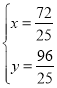 ,
,
即点F的坐标为(![]() ,
,![]() ),
),
∴点N的坐标为(![]() ,
,![]() ),
),
综上所述,满足条件的点N的坐标为(4,3)或(![]() ,
,![]() ).
).


【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
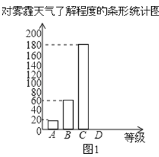
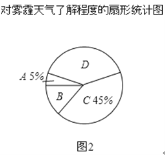
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.