��Ŀ����
����Ŀ����֪������![]() ��
��![]() ���ڵ㣨0��0���͵�
���ڵ㣨0��0���͵�![]() ��������
��������![]() ��
��![]() ���ڵ㣨0��0���͵�
���ڵ㣨0��0���͵�![]() ��������
��������![]() ��
��![]() ���ڵ㣨0��0���͵�
���ڵ㣨0��0���͵�![]() �����˹��ɣ�������
�����˹��ɣ�������![]() ��
��![]() ���ڵ㣨0��0���͵�
���ڵ㣨0��0���͵�![]() ������nΪ�������������ǰ�������
������nΪ�������������ǰ�������![]() ��Ϊϵ��Ϊ
��Ϊϵ��Ϊ![]() �ġ�����ԭ��λ�ơ����������壮
�ġ�����ԭ��λ�ơ����������壮
��1�������![]() ��ֵ��
��ֵ��
��2�����ú�n�Ĵ���ʽ��ʾ�߶�![]() �ij���
�ij���
��3��̽���������⣺
��������![]() �Ķ���������
�Ķ���������![]() ��a��n�к�������ϵ����˵�����ɣ�
��a��n�к�������ϵ����˵�����ɣ�
����ϵ��Ϊa�ġ�����ԭ��λ�ơ�����������ĸ����������Ϊ��T��S������ֱ��д��S��T������ĺ�����ϵʽ��
���𰸡���1��2 ��2��![]() ��3���ټ����� ��
��3���ټ����� ��![]()
��������
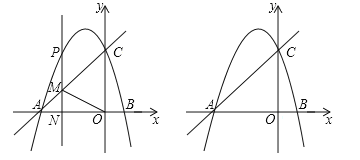
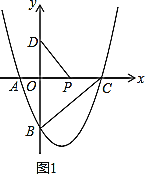
��1������������C1��y1=a(x-1)2+k1��a��0����x���ڵ㣨0��0�����Գ���Ϊֱ��x=1���ɵ���������x�����һ�����㣬��һ���õ�b1��ֵ��
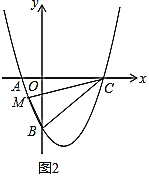
��2�����루1����ͬ�ķ����ɵ�bn=2n����An-1An=bn-bn-1����
��3�����ɣ�1��ͬ���ķ�����֪��k3=-16a��k4=-64a�����˹��ɿ�֪��kn��a��n��������ϵ��
�ڸ�����������Ķ�������S��T֮��Ĺ�ϵ������⣮
�⣺��1����������C1��y1=a��x��1��2+k1��a��0����x���ڵ㣨0��0�����Գ���Ϊֱ��x=1��
����������x�����һ������Ϊ��2��0����
��b1=2��
�ʴ�Ϊ��2.
��2�����루1����ͬ�ķ����ɵ�b2=4��b3=8��b4=16��
���˹��ɿɵ�bn=2n��
��An��1An=bn��bn��1=2n��2n��1=2n��1��
�ʴ�Ϊ��2n��1
��3����kn��a��n��������ϵΪ��kn=��4n��1a��
�������£��ɣ�1������0��0������y1=a��x��1��2+k1���ɵ�k1=��a��
��b1=2��
��C2��y2=a��x��b1��2+k2�ɻ�ΪC2��y2=a��x��2��2+k2��
��������C2��y2=a��x��2��2+k2��x����㣨0��0����
��0=a��0��2��2+k2��
��4a+k2=0����k2=��4a��
��ͬ���ķ�����֪��k3=��16a��k4=��64a��
���˹��ɿ�֪��kn��a��n��������ϵΪ��kn=��4n��1a
�ʴ�Ϊ��kn=��4n��1a.
����������֪��![]() �Ķ�������Ϊ��
�Ķ�������Ϊ��![]()
����![]() ��
�� ![]() ��
��
��������Ķ�������S��T������ĺ�����ϵʽΪ��![]() .
.
�ʴ�Ϊ��![]() .
.

����Ŀ��ijУ�����ˡ�3D����ӡ����ѧʷ��ʫ�����͡�������������У���γ̣�Ϊ�˽�ѧ����������У���γ̵�ϲ���������ѧ������������ʾ����飨�ʾ��������ͼ��ʾ�����������������������ͼ1��ͼ2��������������ͳ��ͼ����
У���γ� | ��Ƶ�� | ��Ƶ�� |
A | 36 | 0.45 |
B | �� | 0.25 |
C | 16 | b |
D | 8 | �� |
���ϼ� | a | 1 |
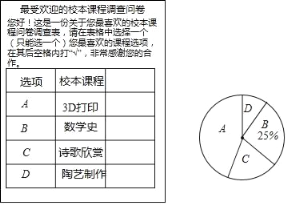
��������ͼ�����ṩ����Ϣ�ش��������⣺
��1��ͳ�Ʊ��е�a���� ����b���� ����
��2����D����Ӧ���ε�Բ�Ľ�Ϊ�� ���ȣ�
��3�����ݵ��������������Ƹ�У2000��ѧ������ϲ������ѧʷ��У���γ̵�������
��4��С����С���μ�У���γ�ѧϰ����ÿ�˴ӡ�A������B������C������У���γ������ѡȡһ�ţ����û���״ͼ���б���ķ�����������ǡ��ѡ��ͬһ��У���γ̵ĸ��ʣ�