题目内容
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
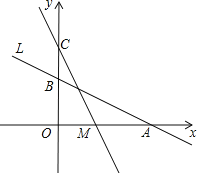
.![]() 是直线
是直线![]() 上的一个动点,直线
上的一个动点,直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() .
.
(1)求这个抛物线的解析式;
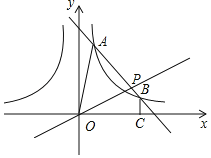
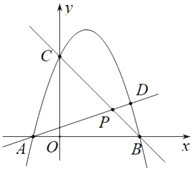
(2)如图,当点![]() 在线段
在线段![]() 上时,连接
上时,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
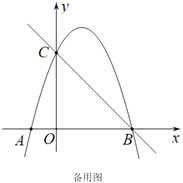
(3)若![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的横坐标为1,2,
的横坐标为1,2,![]() ,
,![]() .
.
【解析】
(1)将![]() ,
,![]() 代入
代入![]() 求
求![]() ;(2)作
;(2)作![]() ,垂足为
,垂足为![]() ,分别过
,分别过![]() ,
,![]() 作
作![]() 轴的垂线
轴的垂线![]() 和平行线
和平行线![]() ,两线交于点
,两线交于点![]() ,得出
,得出![]() ,再根据
,再根据![]() ,设坐标建立等量关系求出
,设坐标建立等量关系求出![]() 点坐标,再求出直线
点坐标,再求出直线![]() 的函数解析式,联立解方程求出
的函数解析式,联立解方程求出![]() 点坐标;(3)分类讨论,利用相似三角形的模型求解.
点坐标;(3)分类讨论,利用相似三角形的模型求解.
(1)将![]() ,
,![]() 代入
代入![]()
得:![]() 解得
解得![]()
∴二次函数的解析式为:![]() ;
;
(2)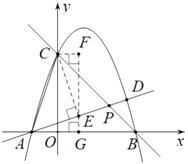
作![]() ,垂足为
,垂足为![]() ,分别过
,分别过![]() ,
,![]() 作
作![]() 轴的垂线
轴的垂线![]() 和平行线
和平行线![]() ,两线交于点
,两线交于点![]() .
.
∵![]() ,∴
,∴![]() .
.
易证![]() ,∴
,∴![]() .设
.设![]() 为
为![]() ,则
,则![]() ,
,![]() ,
,
![]() .
.
∴ ,解得
,解得![]() ,∴点
,∴点![]() .
.
由![]() ,
,![]() 可求得直线
可求得直线![]() 为:
为:![]() ;
;
由![]() ,
,![]() 可求得直线
可求得直线![]() 为:
为:![]() ;
;
二者联立方程组,
解得点![]() 的坐标为
的坐标为![]() ;
;
(3)直线![]() 的解析式为:
的解析式为:![]() 且
且![]() .设
.设![]() 如图:
如图:

①当![]() 在
在![]() 的左侧时:作
的左侧时:作![]() 于
于![]() ,
,![]() 于
于![]()
∴![]() ,
,![]()
∴![]()
∴![]() 代入
代入![]()
解得:![]()
∴ 将![]() 代入则
代入则![]() 的横坐标为1或2;
的横坐标为1或2;
②当![]() 在
在![]() 的右侧时,
的右侧时,![]()
∴![]() 是
是![]() 的中点,设
的中点,设![]() ,
,![]()
∴中点![]() 代入
代入![]()
解得:![]()
将![]() 代入则
代入则![]() 的横坐标为
的横坐标为![]() 或
或![]()
综上所述:点![]() 的横坐标为1,2,
的横坐标为1,2,![]() ,
,![]() .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目