题目内容
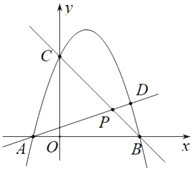
【题目】如图,已知将反比例函数![]() (x<0),沿y轴翻折得到反比例函数
(x<0),沿y轴翻折得到反比例函数![]() (x>0),一次函数y=ax+b与
(x>0),一次函数y=ax+b与![]() 交于A(1,m),B(4,n)两点;
交于A(1,m),B(4,n)两点;
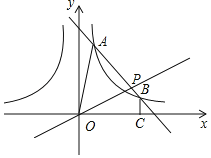
(1)求反比例函数y2和一次函数y=ax+b的解析式;
(2)连接OA,过B作BC⊥x轴,垂足为C,点P是线段AB上一点,若直线OP将四边形OABC的面积分成1:2两部分,求点P的坐标.
【答案】(1)![]() ,y=﹣x+5;(2)P的坐标是P
,y=﹣x+5;(2)P的坐标是P![]() 或P
或P![]() .
.
【解析】
(1)根据翻折的特点求出双曲线y2的解析式;根据A、B两点坐标求直线解析式;
(2)设y=﹣x+5与x轴交于点G,则G(5,0),过A作AD⊥x轴于点D,过P作PE⊥x轴于点E,设P(x,﹣x+5),则PE=﹣x+5,S四边形OPBC=S△POG﹣S△BCG![]() x+12;S△POA=S△AOG﹣S△POG
x+12;S△POA=S△AOG﹣S△POG![]() x
x![]() ,分两种情况列出方程,解方程即可求得P点的坐标.
,分两种情况列出方程,解方程即可求得P点的坐标.
(1)∵反比例函数y1![]() (x<0)与反比例函数y2
(x<0)与反比例函数y2![]() (x>0)关于y轴对称,∴k=﹣(﹣4)=4,∴y2
(x>0)关于y轴对称,∴k=﹣(﹣4)=4,∴y2![]() ,把A(1,m),B(4,n)代入y2
,把A(1,m),B(4,n)代入y2![]() 得:m=4,n=1,∴A(1,4),B(4,1),∴把A(1,4),B(4,1)代入y=ax+b得:
得:m=4,n=1,∴A(1,4),B(4,1),∴把A(1,4),B(4,1)代入y=ax+b得:![]() ,∴
,∴![]() ,∴一次函数的解析式为y=﹣x+5;
,∴一次函数的解析式为y=﹣x+5;
(2)设y=﹣x+5与x轴交于点G,则G(5,0),过A作AD⊥x轴于点D,过P作PE⊥x轴于点E,设P(x,﹣x+5),则PE=﹣x+5.
∵S四边形OPBC=S△POG﹣S△BCG![]() 5(﹣x+5)
5(﹣x+5)![]() (5﹣4)×1
(5﹣4)×1![]() x+12;S△POA=S△AOG﹣S△POG
x+12;S△POA=S△AOG﹣S△POG![]() 5×4
5×4![]() 5(﹣x+5)
5(﹣x+5)![]() x
x![]() ,分两种情况讨论:
,分两种情况讨论:
①若S四边形OPBC=2S△POA时,∴![]() x+12=2(
x+12=2(![]() x
x![]() ),解得:x
),解得:x![]() ,∴P(
,∴P(![]() ,
,![]() );
);
②若2S四边形OPBC=S△POA时,则2(![]() x+12)
x+12)![]() x
x![]() ,解得x
,解得x![]() ,∴P(
,∴P(![]() ,
,![]() );
);
∴当直线OP将四边形OABC的面积分成1:2两部分时,点P的坐标是P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() ).
).

【题目】下表是2018年三月份某居民小区随机抽取20户居民的用水情况::
月用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
统计量名称 | 众数 | 中位数 | 平均数 |
数据 |
|
|
|
(3)为了倡导“节约用水绿色环保”的意识,江赣市自来水公司实行“梯级用水、分类计费”,价格表如下:
月用水梯级标准 | Ⅰ级(30吨以内) | Ⅱ级(超过30吨的部分) |
单价(元/吨) | 2.4 | 4 |
如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭在Ⅰ级标准?
(4)按上表收费,如果某用户本月交水费120元,请问该用户本月用水多少吨?
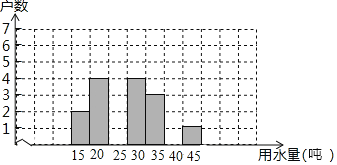
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.
学生借阅图书的次数:
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次以上 |
人数 | 7 | 13 |
| 10 | 3 |

请你根据统计图表中的信息,解答下列问题:
(1)![]() ____________,
____________,![]() ____________;
____________;
(2)该调查统计数据的中位数是___________次;
(3)扇形统计图中,“3次”所对应扇形的圆心角的度数是____________;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.