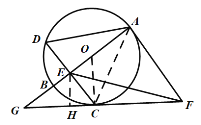
题目内容
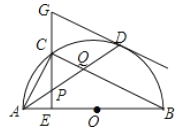
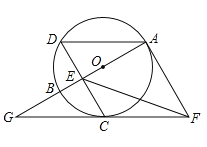
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,若
,若![]() 的半径为4,求
的半径为4,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接![]() ,首先根据垂径定理及
,首先根据垂径定理及![]() 证明
证明![]() 为等边三角形,则有
为等边三角形,则有![]() ,进而可得出
,进而可得出![]() ,再利用平行线的性质和
,再利用平行线的性质和![]() ,证明
,证明![]() ,从而结论可证;
,从而结论可证;
(2)作![]() 于点
于点![]() ,首先证明四边形
,首先证明四边形![]() 为菱形,则有
为菱形,则有![]() ,
,![]() ,再利用平行线的性质进一步得出
,再利用平行线的性质进一步得出![]() ,然后利用特殊角的三角函数值求出EC,CF的长度,从而可求EH,FH,最后利用勾股定理求EF的长度即可.
,然后利用特殊角的三角函数值求出EC,CF的长度,从而可求EH,FH,最后利用勾股定理求EF的长度即可.
(1)证明:如图,连接![]() ,
,
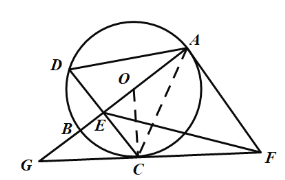
∵![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() .
.
![]() ,
,
![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 与
与![]() 相切.
相切.
(2)解:如图,作![]() 于点
于点![]() ,
,
∵![]() 与
与![]() 相切,
相切,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∵![]() ,
,
∴四边形![]() 为菱形,
为菱形,
∴![]() ,
,![]() ,
,
![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ,
,![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() .
.

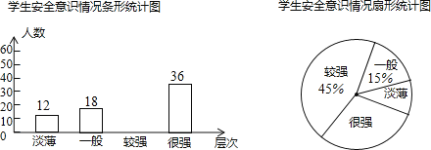
【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?