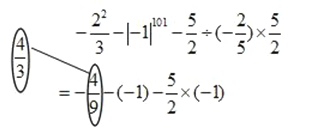题目内容
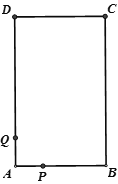
【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D回到点A,设点P的运动时间为t秒,
(1)当t=3秒时,求BP的长;
(2)当t为何值时,连接BP,AP,△ABP的面积为长方形的面积三分之一?
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等?

【答案】(1)2;(2)4秒或8秒;(3)t=2.5秒,4.5秒,7.5秒或9.5秒.
【解析】
(1)当t=3秒时,点P运动到线段BC上,即可得到BP的长度;
(2)由△ABP的面积为长方形的面积三分之一,则分为点P在BC上和点P在AD上两大类进行讨论,即可得到答案;
(3)根据题意,要使得一个三角形与△DCQ全等,则点P的位置可以有四个,即点P分别运动到P1,P2,P3 ,P4时,有△DCP1,△ABP2,△ABP3,△DCP4与△DCQ全等,根据P点运动的位置,即可计算出时间.
解:(1)当t=3秒时,
点P走过的路程为:![]() ,
,
∵AB=4,
∴点P运动到线段BC上,
∴BP=6-4=2;
(2)∵矩形ABCD的面积=![]() ,
,
∴△ABP的面积=![]() ,
,
∵AB=4,
∴△ABP的高为:![]() ,
,
如图:
当点P在BC上时,有BP=4,
∴时间为:![]() s;
s;
当点P在AD上时,有AP=4,
∴时间为:![]() s;
s;
∴当时间t=4s或t=8s时,△ABP的面积为长方形的面积三分之一;
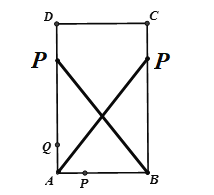
(3)根据题意,如图,连接CQ,有AB=CD=4,∠A=∠B=∠C=∠D=90°,DQ=5,
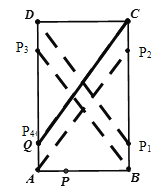
∴要使得一个三角形与△DCQ全等,则另一直角边必须等于DQ.
①当点P运动到P1时,CP1=DQ=5,此时△DCQ≌△CDP1,
∴点P的路程为:AB+BP1=4+1=5,
∴时间![]() ;
;
②当点P运动到P2时,BP2= DQ=5,此时△CDQ≌△ABP2,
∴点P的路程为:AB+BP2=4+5=9,
∴时间![]() ;
;
③当点P运动到P3时,AP3= DQ=5,此时△CDQ≌△ABP3,
∴点P的路程为:AB+BC+CD+DP3=4+6+4+1=15,
∴时间![]() ;
;
④当点P运动到P4时,即P与Q重合时,DP4=DQ=5,△CDQ≌△CDP4,
∴点P的路程为:AB+BC+CD+DP4=4+6+4+5=19,
∴时间![]() ;
;
综合上述,时间t的值可以是:t=2.5秒,4.5秒,7.5秒或9.5秒.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案