题目内容
【题目】已知关于x的一元二次方程mx2+(3m+1)x+3=0.
(1)当m取何值时,此方程有两个不相等的实数根;
(2)当抛物线y=mx2+(3m+1)x+3与x轴两个交点的横坐标均为整数,且m为正整数时,求此抛物线的解析式;
(3)在(2)的条件下,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象直接写出实数a的取值范围.
【答案】(1)当m≠![]() 且m≠0时,方程有两个不相等的实数根;(2)y=x2+4x+3;(3) 当y1>y2时,a>1,或a<-5.
且m≠0时,方程有两个不相等的实数根;(2)y=x2+4x+3;(3) 当y1>y2时,a>1,或a<-5.
【解析】
(1)根据一元二次方程的定义和一元二次方程根的判别式进行分析解答即可;
(2)用公式法求得关于x的一元二次方程mx2+(3m+1)x+3=0的两根,再结合已知条件求得m的值即可得到抛物线的解析式;
(3)根据(2)中所得抛物线的解析式,画出函数的图象,根据图象结合已知条件即可求得对应的a的取值范围.
(1)由题意可知,Δ=b2-4ac=(3m+1)2-4m×3=(3m-1)2>0,
解得:m≠![]() ,
,
∵mx2+(3m+1)x+3=0是一元二次方程,
∴m≠0,
∴当m≠![]() 且m≠0时,关于x的一元二次方程mx2+(3m+1)x+3=0有两个不相等的实数根;
且m≠0时,关于x的一元二次方程mx2+(3m+1)x+3=0有两个不相等的实数根;
(2)由一元二次方程的求根公式可解得mx2+(3m+1)x+3=0的两实数根为:x1=-3,x2=![]() .
.
∵抛物线与x轴两个交点的横坐标均为整数,且m为正整数,
∴m=1,
∴抛物线的解析式为y=x2+4x+3;
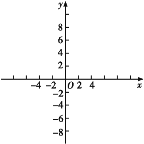
(3)画出函数y=x2+4x+3的图象如下图所示;
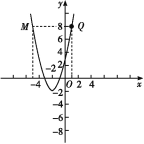
当x=1时,y=1+4+3=8,由此可得图中点Q的坐标为(1,8),
过点Q作y轴的垂线,交抛物线于点M,
根据抛物线的对称性,可得点M(-5,8),
由图象可知,当y1>y2时,a>1,或a<-5.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
【题目】陶军于上周购买某农产品10000斤,每斤![]() 元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤
元进入批发市场后共占5个摊位.每个摊位最多容纳2000斤该品种的农产品,每个摊位的市场管理价位为每天20元,下表为本周内该农产品每天的批发价格比前一天的涨跌情况(购进当日该农产品的批发价格为每斤![]() 元)
元)
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天的价格涨跌情况(元) |
|
|
|
|
|
当天的交易量(斤) | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品价格为每斤多少元?
(2)本周内该农产品的最高价格为每斤多少元?最低价格为每斤多少元?
(3)陶军在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
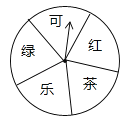
【题目】共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利.但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”.随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).
调查结果分组统计表
组别 | 观点 | 频数(人数) |
| 损坏零件 | 50 |
| 破译密码 | 20 |
| 乱停乱放 |
|
| 私锁共享单车,归为己用 |
|
| 其他 | 30 |
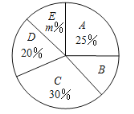
请根据以上信息,解答下列问题:
(1)填空:![]() ;
;![]() ;
;![]() ;
;
(2)求扇形图中![]() 组所在扇形的圆心角度数;
组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有![]() 组观点的市民人数.
组观点的市民人数.
(4)针对以上现象,作为初中生的你有什么合理化的建议.