��Ŀ����
����Ŀ���ڱ߲���ȵ�ƽ���ı���ֽƬ����ȥһ�����Σ�����һ���ı��Σ���Ϊ��һ�β����������µ��ı���ֽƬ���ټ�ȥһ�����Σ�������һ���ı��Σ���Ϊ�ڶ��β����������������ƣ�����n�β������µ��ı��������Σ����ԭƽ���ı���Ϊn�����Σ���ͼ1����ABCD�У���AB��1��BC��2������ABCDΪ1�����Σ�
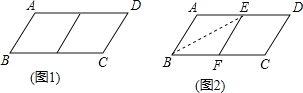
��1�����������
���ڱ߳��ֱ�Ϊ2��3��ƽ���ı����� ��������
��С��Ϊ�˼�ȥһ�����Σ��������²�������ͼ2������ABCD��BE�۵�����E��AD�ϣ���ʹ��A����BC���ϵĵ�F���õ��ı���ABFE����֤���ı���ABEF�����Σ�
��2��������̽������㣺
����֪��ABCD���ڱ߳��ֱ�Ϊ1��a��a��1��������3�����Σ��뻭����ABCD���ü��ߵ�ʾ��ͼ������ͼ���·�д��a��ֵ��
����֪��ABCD���ڱ߳��ֱ�Ϊa��b��a��b��������a��6b��r��b��5r��r��0��������ABCD
�� ��������
���𰸡���1����2���ڼ�������2���ټ���������10�����ɣ�
����Ϊa��6b��r��b��5r������a=6��5r+r=31r��b=5r����ͼ��ʾ��ƽ���ı���ABCD��10������.

�����������������
��1���������������Ķ���ش�����ƽ����+��ƽ���ߵĽṹ֤����ABE�ǵ�������������2���������������Ķ��弰���ε��ж���ͼ�����ҳ�a��b��������ϵ������ͼ��.
������1����2��
�����۵�֪����ABE=��FBE��AB=BF��
���ı���ABCD��ƽ���ı��Σ�
��AE��BF�����AEB=��FBE��
���AEB=��ABE����AE=AB��
��AE=BF��
���ı���ABFE��ƽ���ı��Σ�
���ı���ABFE�����Σ�
��2������ͼ��ʾ��

����Ϊa��6b��r��b��5r������a=6��5r+r=31r��b=5r����ͼ��ʾ��ƽ���ı���ABCD��10������.


 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�