Question

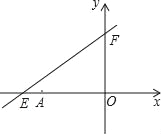
【题目】如图，直线y=kx+6与x轴、y轴分别交于点E、F，点E的坐标为（﹣8，0），点A的坐标为（﹣6，0）．

（1）求k的值；

（2）若点P（x，y）是第二象限内的直线上的一个动点，在点P的运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；

（3）探究：在（2）的情况下，当点P运动到什么位置时，△OPA的面积为，并说明理由．

Answer 1

【答案】（1）k= （2）﹣8＜x＜0（3）（﹣， ）

【解析】试题分析：（1）将点E坐标（-8，0）代入直线y=kx+6就可以求出k值，从而求出直线的解析式；

（2）由点A的坐标为（-6，0）可以求出OA=6，求△OPA的面积时，可看作以OA为底边，高是P点的纵坐标的绝对值．再根据三角形的面积公式就可以表示出△OPA．从而求出其关系式；根据P点的移动范围就可以求出x的取值范围．

（3）根据△OPA的面积为代入（2）的解析式求出x的值，再求出y的值就可以求出P点的位置．

（1）∵点E（﹣8，0）在直线y=kx+6上，

∴0=﹣8k+6，

∴k=；

（2）∵k=，

∴直线的解析式为：y=x+6，

∵P点在y=x+6上，设P（x， x+6），

∴△OPA以OA为底的边上的高是|x+6|，

当点P在第二象限时，|x+6|=x+6，

∵点A的坐标为（﹣6，0），

∴OA=6．

∴S==x+18．

∵P点在第二象限，

∴﹣8＜x＜0；

（3）设点P（m，n）时，其面积S=，

则，

解得|n|=，

则n1=或者n2=﹣（舍去），

当n=时， =m+6，

则m=﹣，

故P（﹣，）时，三角形OPA的面积为．