题目内容
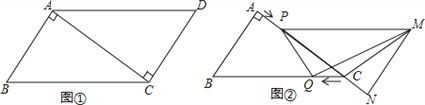
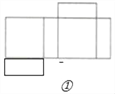
【题目】学习了“展开与折叠”后,同学们了解了一些简单几何体的展开图,小明在家用剪刀剪一个如图(1)的长方体纸盒,但不小心多剪开了一条棱,得到图(2)中的纸片①和②,请解答下列问题:
(1)小明共剪开 条棱;
(2)现在小明想将剪断的纸片②拼接到纸片①上,构成该长方体纸盒的展开图,请你在①中画出纸片②的一种位置;
(3)请从A,B两题中任选一题作答.
A.若长方体纸盒的长,宽,高分别为m,m,n(单位:cm,m>n),求(2)中展开图的周长.
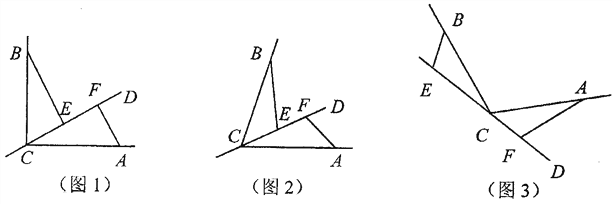
B.若长方体纸盒的长,宽,高分别是a,b,c(单位:cm,a>b>c),如图(3),画出它的展开图中周长最大时的展开图,并求出周长(用含a,b,c的式子表示)

【答案】(1)8(2)四种情况(3).A、①③的周长为6m+8n;②④的周长为8m+6n;B 、画图见解析,周长为2c+4b+8a.
【解析】试题分析:(1)根据平面图形得出剪开棱的条数;
(2)根据长方体的展开图的情况可知有四种情况;
(3)A、观察(2)中的展开图分别进行计算即可得;
B、展开平面图求周长的公式与展开的方式无关 所以无论怎么展开我们通过实践都可以得出以下结论:假设长,宽,高分别为x,y,z(x,y,为任意值)周长c=2x+4y+8z,
这个平面图的周长最大也就是当x最小,z最大.即c=2c+4b+8a,
这个平面图的周长最小也就是当x最大,z最小.即c=2a+4b+8c.
试题解析:(1)小明共剪了8条棱,
故答案为:8;
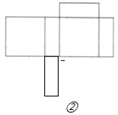
(2)如图,四种情况.
 ,
,
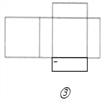 ,
,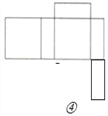 ;
;
(3)A、①、③的周长为6m+8n;②、④的周长为8m+6n;
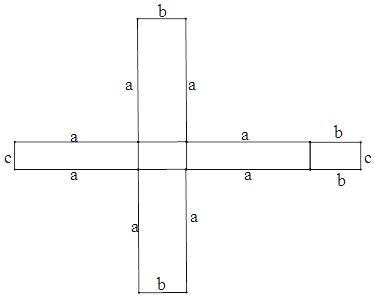
B、展开图如图所示,
周长为:2c+4b+8a.

练习册系列答案
相关题目