Question

【题目】如图，抛物线y=-x2+bx+c的顶点为C(3，4)，交x轴于点A，B(点B在点A的右侧)，点P在第一象限，且在抛物线AC部分上，PD⊥PC交x轴于点D。

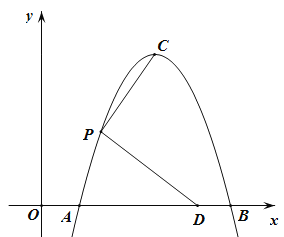
（1）求该抛物线的表达式；

（2）若PD=3PC，求OD的长.

Answer 1

【答案】（1）y=-x2+6x-5；（2）OD= 5.

【解析】

（1）已知顶点坐标，现知a值，直接用顶点法即可求出抛物线的解析式；

（2）先求出抛物线与x轴的交点坐标，设P（p，-+6p-5）(1≤p≤3)，先证明△Rt△PCF∽Rt△PED，根据相似三角形的性质列比例式，求出p值，然后根据C、F两点的纵坐标，求得CF的长，则由相似的性质即可得出ED的长，则OD的长可知.

解：

（1）由题意得，y=-(x-3)2+4=-x2+6x-5；

（2）设y=-x2+6x-5=(x-1)(-x+5)=0，

解得x=1或5，

∴A（1，0），B（5，0），

如图，过点P作PE∥y轴交x轴于点E，过P作PF平行x轴交对称轴于F，

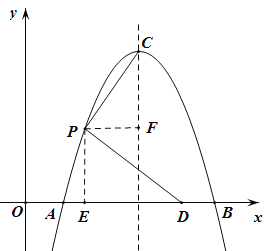
设P（p，-p2+6p-5）(1≤p≤3)，

∴∠PFC=∠PED=90°

∵∠CPF+∠FPD=∠EPD+∠FPD=90°，

∵∠CPF=∠DPE，

∴∠PFC=∠PDE，

又∵∠PFC=∠PED=90°

∴Rt△PCF∽Rt△PDE，

∴ ，

∴，ED=3CF

整理得p2-9p+14=0，

(p-2)(p-7)=0，

∴p=2, 或P=7（舍去），

∴P（2，3），

CF=yC-yF=4-3=1，

∴ED=3CF=3，

∴OD=OE+ED=2+3=5.