题目内容
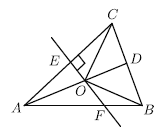
【题目】如图,在△ABC中,D是BC边的中点,DE⊥BC交AB于点E,AD=AC,EC交AD于点F.
(1)求证:△ABC∽△FCD;
(2)求证:FC=3EF.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由AD=AC,利用等边对等角得到一对角相等,再由已知角相等,利用两对对应角相等的三角形相似即可得证;
(2)根据相似三角形的性质得到![]() ,由D是BC边的中点,得到BC=2CD,于是得到AD=AC=2FD,由于∠ACD=∠ADC,∠B=∠FCD,推出∠EAD=∠ACE,得到△EAF∽△ECA,根据相似三角形的性质得到
,由D是BC边的中点,得到BC=2CD,于是得到AD=AC=2FD,由于∠ACD=∠ADC,∠B=∠FCD,推出∠EAD=∠ACE,得到△EAF∽△ECA,根据相似三角形的性质得到![]() ,即可得到结论.
,即可得到结论.
(1)∵AD=AC,
∴∠ADC=∠ACB,
∵∠B=∠ECB,
∴△ABC∽△FCD;
(2)∵△ABC∽△FCD,
∴ ![]() ,
,
∵D是BC边的中点,
∴BC=2CD,
∴AD=AC=2FD,
∵∠ACD=∠ADC,∠B=∠FCD,
∴∠EAD=∠ACE,
∴△EAF∽△ECA,
∴![]() ,
,
∴EC=2EA=4EF,
∴FC=3EF.

练习册系列答案
相关题目