��Ŀ����
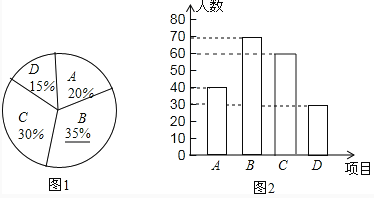
����Ŀ��Ϊӭ��ʮ���ˣ�ijУ������A������B�����C��������D�������������������Ϊ�˽�ѧ�����������������ϲ���������ȫУ��Χ�������ȡ������ѧ���������ʾ����飨ÿ���������ͬѧ����ѡ�����ֻ����4���������ѡ��һ�֣��������ݽ������������Ƴ���������ͳ��ͼ��δ����������
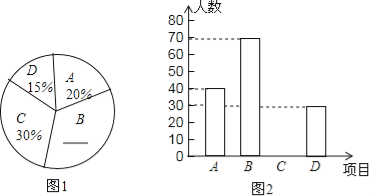
��1����ε����У�һ�������� ����ѧ����
��2���벹ȫ����ͳ��ͼ��
��3������3����ϲ������˶���ѧ����1����ϲ�������˶���ѧ���������μ�һ�����껥���������ѡ��2�˵����鳤�������������������˾�����ϲ������˶���ѧ���ĸ��ʣ�
���𰸡���1��200����2����ͼ����������3��![]() .
.
��������
��1������A�����������ռ�İٷֱȣ����������������
��2��������1��ȥA��C��D����ռ�İٷֱȣ��������B��ռ�İٷֱȣ���������������ռ�İٷֱȣ����C���������Ӷ���ȫͼ�Σ�
��3��������������оٷ����ٳ����еĿ��ܣ�ע��Ҫ�������ز�©���ٸ��ݸ��ʹ�ʽ���ɵó��𰸣�
��1���������ѧ����![]() =200��������
=200��������
�ʴ�Ϊ200��
��2��B��ռ�İٷֱ���1-15%-20%-30%=35%��
C�������ǣ�200��30%=60��������
��ͼ���£�
��3����A1��A2��A3��ʾ3��ϲ������˶���ѧ����B��ʾ1�������˶���ѧ����
���4����ѡ��2�˵�����У���A1��A2������A1��A3������A1��B������A2��A3������A2��B������A3��B��������6�֣�
ѡ����2�˶�����ϲ������˶���ѧ���У�A1��A2������A1��A3������A2��A3������3�֣�
�����˾�����ϲ������˶���ѧ���ĸ���![]() ��
��